آموزش الگوریتم درخت تصمیم در یادگیری ماشین با پایتون

0 دیدگاه

الگوریتم درخت تصمیم یک الگوریتم سلسله‌مراتبی مبتنی بر ساختار درخت است که برای طبقه‌بندی یا پیش‌بینی نتایج بر اساس مجموعه‌ای از قوانین به‌کار می‌رود. این الگوریتم داده‌ها را بر اساس مقادیر ویژگی‌های ورودی به زیرمجموعه‌هایی تقسیم می‌کند. روند تقسیم به‌صورت بازگشتی ادامه می‌یابد تا زمانی که داده‌های هر زیرمجموعه به یک کلاس تعلق داشته باشند یا برای متغیر هدف یک مقدار یکسان داشته باشند. در نهایت، درخت حاصل مجموعه‌ای از قواعد تصمیم‌گیری است که می‌توان از آن برای پیش‌بینی یا طبقه‌بندی داده‌های جدید استفاده کرد.

الگوریتم درخت تصمیم در هر گره بهترین ویژگی را برای تقسیم داده‌ها انتخاب می‌کند. بهترین ویژگی آن است که بیشترین افزایش اطلاعات (Information Gain) یا بیشترین کاهش آنتروپی (Entropy) را ایجاد کند. افزایش اطلاعات معیاری است برای سنجش مقدار اطلاعاتی که با تقسیم داده‌ها بر اساس یک ویژگی خاص به‌دست می‌آید. در حالی که آنتروپی معیاری برای سنجش میزان بی‌نظمی یا آشفتگی داده‌ها است. الگوریتم از این معیارها برای تعیین ویژگی بهینه جهت تقسیم داده‌ها در هر گره استفاده می‌کند.

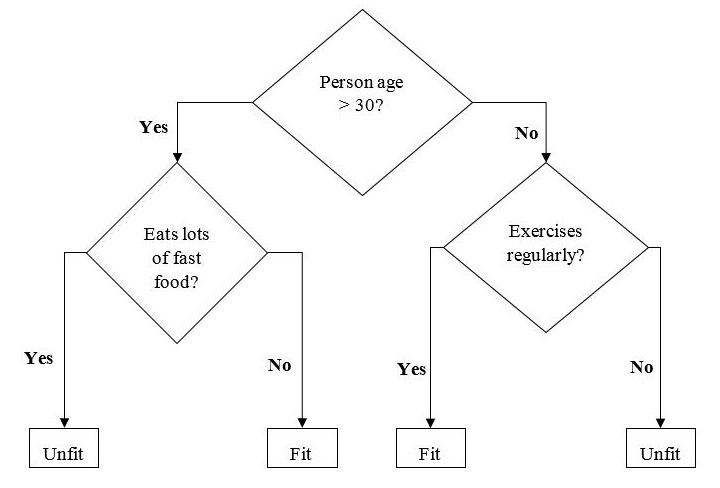
یک نمونه از درخت دودویی (Binary Tree) برای پیش‌بینی این‌که آیا فردی سالم (Fit) یا ناسالم (Unfit) است، بر اساس اطلاعاتی مانند سن، عادات غذایی و عادات ورزشی، در زیر نشان داده شده است:

در الگوریتم درخت تصمیم، پرسش‌ها به‌عنوان گره‌های تصمیم (Decision Nodes) و نتایج نهایی به‌عنوان برگ‌ها (Leaves) شناخته می‌شوند.

انواع الگوریتم درخت تصمیم

دو نوع اصلی از الگوریتم درخت تصمیم وجود دارد:

۱. درخت طبقه‌بندی (Classification Tree) – درخت طبقه‌بندی برای دسته‌بندی داده‌ها در کلاس‌ها یا گروه‌های مختلف استفاده می‌شود. این روش با تقسیم داده‌ها به زیرمجموعه‌ها بر اساس مقادیر ویژگی‌های ورودی کار می‌کند و هر زیرمجموعه را به یک کلاس خاص اختصاص می‌دهد.

۲. درخت رگرسیون (Regression Tree) – درخت رگرسیون برای پیش‌بینی مقادیر عددی یا متغیرهای پیوسته به‌کار می‌رود. این روش داده‌ها را بر اساس مقادیر ویژگی‌های ورودی به زیرمجموعه‌هایی تقسیم کرده و به هر زیرمجموعه یک مقدار عددی اختصاص می‌دهد.

پیاده سازی الگوریتم درخت تصمیم

شاخص جینی (Gini Index)

شاخص جینی نام تابع هزینه‌ای است که برای ارزیابی تقسیم‌های دودویی (Binary Splits) در مجموعه داده به‌کار می‌رود و معمولاً با متغیر هدف دسته‌ای (مانند موفقیت یا شکست) استفاده می‌شود.

هرچه مقدار شاخص جینی بیشتر باشد، همگنی داده‌ها بیشتر است.
مقدار ایده آل شاخص جینی برابر با ۰ است و بدترین مقدار آن ۰٫۵ (برای مسائل دوکلاسه) است.

مراحل محاسبه شاخص جینی برای یک تقسیم:

ابتدا شاخص جینی برای زیرگره‌ها محاسبه می‌شود. فرمول آن به شکل p^2+q^2 است که در آن احتمال موفقیت و احتمال شکست است.
سپس شاخص جینی برای کل تقسیم محاسبه می‌شود. این مقدار برابر با میانگین وزنی امتیاز جینی هر یک از گره‌های آن تقسیم است.

الگوریتم CART (Classification and Regression Tree) از روش جینی برای ایجاد تقسیم‌های دودویی استفاده می‌کند.

ایجاد تقسیم (Split Creation)

تقسیم در واقع شامل یک ویژگی (Attribute) از مجموعه‌داده و یک مقدار مربوط به آن است. برای ایجاد یک تقسیم در مجموعه‌داده، سه بخش اصلی وجود دارد:

بخش ۱: محاسبه امتیاز جینی (Gini Score) – این بخش در قسمت قبل توضیح داده شد و مبنای سنجش کیفیت یک تقسیم محسوب می‌شود.

بخش ۲: تقسیم مجموعه‌داده (Splitting a Dataset) – در این مرحله، مجموعه‌داده به دو لیست از سطرها تقسیم می‌شود که بر اساس شاخص ویژگی و مقدار تقسیم آن ویژگی جداسازی می‌شوند. پس از تشکیل دو گروه (راست و چپ)، می‌توانیم ارزش تقسیم را با استفاده از امتیاز جینی محاسبه‌شده در بخش اول ارزیابی کنیم. مقدار تقسیم مشخص می‌کند که یک ویژگی در کدام گروه قرار می‌گیرد.

بخش ۳: ارزیابی تمام تقسیم‌ها (Evaluating All Splits) – پس از محاسبه امتیاز جینی و انجام تقسیم، باید همه تقسیم‌های ممکن ارزیابی شوند. برای این کار:

ابتدا هر مقدار مرتبط با هر ویژگی به‌عنوان یک کاندیدای تقسیم بررسی می‌شود.
سپس هزینه (Cost) هر تقسیم محاسبه و بهترین تقسیم انتخاب می‌شود.

بهترین تقسیم به‌عنوان یک گره (Node) در درخت تصمیم استفاده خواهد شد.

ساخت درخت (Building a Tree)

همان‌طور که می‌دانیم، یک درخت شامل گره ریشه (Root Node) و گره‌های پایانی (Terminal Nodes) است. بعد از ایجاد گره ریشه، می‌توانیم درخت را در دو مرحله اصلی بسازیم:

بخش ۱: ایجاد گره پایانی (Terminal Node Creation)

در هنگام ایجاد گره‌های پایانی درخت تصمیم، باید مشخص کنیم چه زمانی رشد درخت متوقف شود. این کار بر اساس دو معیار انجام می‌شود:

حداکثر عمق درخت (Maximum Tree Depth): بیشترین تعداد گره‌هایی است که یک درخت می‌تواند پس از گره ریشه داشته باشد. زمانی که درخت به حداکثر عمق برسد، افزودن گره پایانی متوقف می‌شود.
حداقل رکوردهای گره (Minimum Node Records): حداقل تعداد الگوهای آموزشی است که یک گره باید پوشش دهد. اگر تعداد رکوردهای گره کمتر یا مساوی این مقدار شود، دیگر گره پایانی جدیدی اضافه نمی‌شود.

گره پایانی برای پیش‌بینی نهایی استفاده می‌شود.

بخش ۲: تقسیم بازگشتی (Recursive Splitting)

بعد از مشخص کردن شرایط توقف و گروه پایانی، می‌توانیم ساخت درخت را آغاز کنیم. در روش تقسیم بازگشتی:

وقتی یک گره ایجاد می‌کنیم، داده‌های موجود در آن گره را به دو گروه تقسیم می‌کنیم.
سپس برای هر گروه داده، گره‌های فرزند (Child Nodes) را ایجاد می‌کنیم.
برای ساخت هر گره فرزند، همان تابع را دوباره روی داده‌های آن گروه فراخوانی می‌کنیم.
این فرآیند به‌طور پیوسته ادامه پیدا می‌کند تا درخت کامل شود.

پیش‌بینی (Prediction)

وقتی درخت تصمیم ساخته شد، می‌توانیم با استفاده از آن پیش‌بینی انجام دهیم. برای پیش‌بینی:

یک سطر داده به درخت داده می‌شود.
الگوریتم مقدار ویژگی‌ها را بررسی می‌کند و مسیر مناسب را در درخت دنبال می‌کند.
اگر مقدار ویژگی با شرط گره مطابقت داشته باشد، الگوریتم به شاخه چپ حرکت می‌کند؛ در غیر این صورت به شاخه راست می‌رود.
این روند ادامه پیدا می‌کند تا داده به یک گره پایانی برسد و پیش‌بینی انجام شود.

فرضیات (Assumptions)

هنگام ساخت درخت تصمیم، چند فرض اصلی را در نظر می‌گیریم:

مجموعه داده آموزشی به‌عنوان گره ریشه آغاز کار درخت قرار می‌گیرد.
الگوریتم درخت تصمیم ویژگی‌ها را به‌صورت دسته‌ای (Categorical) ترجیح می‌دهد. اگر ویژگی‌ها پیوسته باشند، ما آن‌ها را پیش از ساخت مدل گسسته‌سازی (Discretization) می‌کنیم.
رکوردها بر اساس مقادیر ویژگی‌ها به‌طور بازگشتی بین گره‌ها توزیع می‌شوند.
الگوریتم برای تعیین جایگاه ویژگی‌ها در گره ریشه یا گره‌های داخلی، از روش‌های آماری استفاده می‌کند.

پیاده‌سازی در پایتون (Implementation in Python)

در این بخش، الگوریتم درخت تصمیم را با استفاده از زبان پایتون و مجموعه‌داده معروف Iris پیاده‌سازی می‌کنیم. این مجموعه‌داده شامل ۱۵۰ نمونه گل زنبق است که هر نمونه دارای چهار ویژگی می‌باشد: طول کاسبرگ (Sepal Length)، عرض کاسبرگ (Sepal Width)، طول گلبرگ (Petal Length) و عرض گلبرگ (Petal Width). گل‌ها به سه کلاس تعلق دارند: Setosa، Versicolor و Virginica.

ابتدا کتابخانه‌های لازم را وارد کرده و مجموعه‌داده Iris را بارگذاری می‌کنیم:

import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier

# Load the iris dataset
iris = load_iris()

# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(iris.data,
iris.target, test_size=0.3, random_state=0)

import numpy as np

from sklearn.datasets import load_iris

from sklearn.model_selection import train_test_split

from sklearn.tree import DecisionTreeClassifier

# Load the iris dataset

iris = load_iris()

# Split the dataset into training and testing sets

X_train, X_test, y_train, y_test = train_test_split(iris.data,

iris.target, test_size=0.3, random_state=0)

سپس یک نمونه از طبقه‌بند درخت تصمیم ایجاد کرده و آن را روی داده‌های آموزشی آموزش می‌دهیم:

# Create a Decision Tree classifier
dtc = DecisionTreeClassifier()

# Fit the classifier to the training data
dtc.fit(X_train, y_train)

# Create a Decision Tree classifier

dtc = DecisionTreeClassifier()

# Fit the classifier to the training data

dtc.fit(X_train, y_train)

بعد از آموزش مدل، از آن برای پیش‌بینی روی داده‌های آزمایشی استفاده می‌کنیم:

# Make predictions on the testing data
y_pred = dtc.predict(X_test)

1 2	# Make predictions on the testing data y_pred = dtc.predict(X_test)

برای ارزیابی عملکرد مدل، دقت (Accuracy) را محاسبه می‌کنیم:

# Calculate the accuracy of the classifier
accuracy = np.sum(y_pred == y_test) / len(y_test)
print("Accuracy:", accuracy)

# Calculate the accuracy of the classifier

accuracy = np.sum(y_pred == y_test) / len(y_test)

print("Accuracy:", accuracy)

در نهایت، درخت تصمیم را با استفاده از کتابخانه Matplotlib ترسیم می‌کنیم:

import matplotlib.pyplot as plt
from sklearn.tree import plot_tree

# Visualize the Decision Tree using Matplotlib
plt.figure(figsize=(20,10))
plot_tree(dtc, filled=True, feature_names=iris.feature_names,
class_names=iris.target_names)
plt.show()

import matplotlib.pyplot as plt

from sklearn.tree import plot_tree

# Visualize the Decision Tree using Matplotlib

plt.figure(figsize=(20,10))

plot_tree(dtc, filled=True, feature_names=iris.feature_names,

class_names=iris.target_names)

plt.show()

تابع plot_tree از ماژول sklearn.tree برای رسم درخت تصمیم به‌کار می‌رود. در این تابع:

پارامتر dtc مدل آموزش‌دیده را مشخص می‌کند.
پارامتر filled=True باعث می‌شود گره‌ها با رنگ پر شوند.
پارامتر feature_names برای نمایش نام ویژگی‌ها استفاده می‌شود.
پارامتر class_names نام کلاس‌های هدف را نشان می‌دهد.
پارامتر figsize اندازه تصویر را تعیین می‌کند.

در نهایت، با فراخوانی تابع show() نمودار درخت نمایش داده می‌شود.

نمونه پیاده‌سازی کامل

در این قسمت، یک نمونه کامل از پیاده‌سازی الگوریتم طبقه‌بندی درخت تصمیم (Decision Tree Classification) در پایتون با استفاده از مجموعه‌داده Iris ارائه می‌کنیم:

import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier

# Load the iris dataset
iris = load_iris()

# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.3, random_state=0)

# Create a Decision Tree classifier
dtc = DecisionTreeClassifier()

# Fit the classifier to the training data
dtc.fit(X_train, y_train)

# Make predictions on the testing data
y_pred = dtc.predict(X_test)

# Calculate the accuracy of the classifier
accuracy = np.sum(y_pred == y_test) / len(y_test)
print("Accuracy:", accuracy)

# Visualize the Decision Tree using Matplotlib
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
plt.figure(figsize=(20,10))
plot_tree(dtc, filled=True, feature_names=iris.feature_names,
class_names=iris.target_names)
plt.show()

import numpy as np

from sklearn.datasets import load_iris

from sklearn.model_selection import train_test_split

from sklearn.tree import DecisionTreeClassifier

# Load the iris dataset

iris = load_iris()

# Split the dataset into training and testing sets

X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.3, random_state=0)

# Create a Decision Tree classifier

dtc = DecisionTreeClassifier()

# Fit the classifier to the training data

dtc.fit(X_train, y_train)

# Make predictions on the testing data

y_pred = dtc.predict(X_test)

# Calculate the accuracy of the classifier

accuracy = np.sum(y_pred == y_test) / len(y_test)

print("Accuracy:", accuracy)

# Visualize the Decision Tree using Matplotlib

import matplotlib.pyplot as plt

from sklearn.tree import plot_tree

plt.figure(figsize=(20,10))

plot_tree(dtc, filled=True, feature_names=iris.feature_names,

class_names=iris.target_names)

plt.show()

خروجی

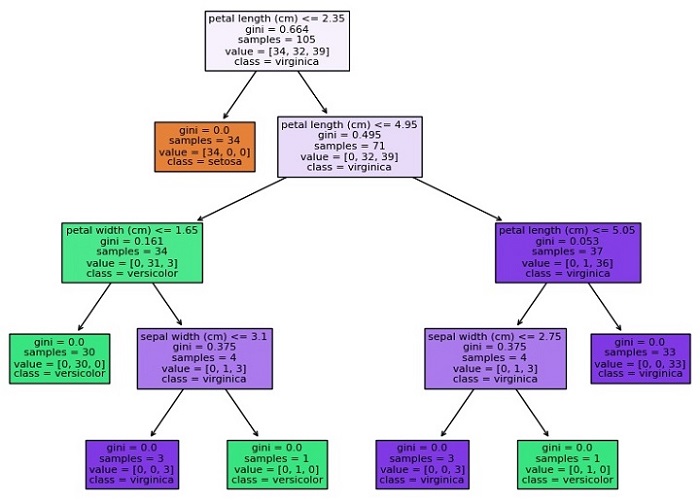
کد بالا نمودار درخت تصمیم را ترسیم می‌کند و نتیجه‌ای مشابه زیر تولید خواهد کرد:

Accuracy: 0.9777777777777777

1	Accuracy: 0.9777777777777777

همانطور که می‌بینید، نمودار، ساختار درخت تصمیم (Decision Tree) را نشان می‌دهد که در آن هر گره نشان‌دهنده یک تصمیم بر اساس مقدار یک ویژگی است و هر گره برگ نشان‌دهنده یک کلاس یا مقدار عددی است. رنگ هر گره نشان‌دهنده کلاس یا مقدار اکثریت نمونه‌ها در آن گره است و اعداد پایین نمودار، تعداد نمونه‌هایی را که به آن گره می‌رسند، نشان می‌دهند.

اگر هنوز با مفاهیم اولیه برنامه‌نویسی آشنا نیستید و می‌خواهید به‌طور اصولی یادگیری پایتون را شروع کنید، بهترین راه شروع، شرکت در دوره تخصصی پایتون است. این دوره به شما کمک می‌کند تا با اصول اولیه پایتون آشنا شوید و به تدریج مهارت‌های لازم برای پیاده‌سازی الگوریتم‌های یادگیری ماشین و پروژه‌های پیچیده را کسب کنید.