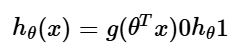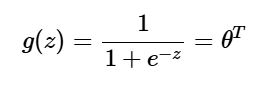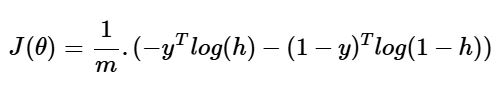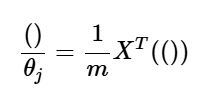آموزش رگرسیون لجستیک در یادگیری ماشین با پایتون

0 دیدگاه

رگرسیون لجستیک در یادگیری ماشین یکی از الگوریتم‌های یادگیری نظارت‌شده در دسته‌بندی است که برای پیش‌بینی احتمال وقوع یک متغیر هدف به کار می‌رود. ماهیت متغیر هدف یا وابسته در این روش، دووجهی (Dichotomous) است. این یعنی تنها دو کلاس یا حالت ممکن برای آن وجود دارد.

به‌بیان ساده، متغیر وابسته دارای دو مقدار ممکن است. مقدار ۱ معمولاً به معنای «موفقیت» یا «بله» و مقدار ۰ به معنای «شکست» یا «خیر» در نظر گرفته می‌شود.

از دیدگاه ریاضی، مدل رگرسیون لجستیک احتمال وقوع رویداد P(Y=1) را به‌عنوان تابعی از X پیش‌بینی می‌کند. این الگوریتم یکی از ساده‌ترین روش‌های یادگیری ماشین (Machine Learning) است که می‌توان از آن در مسائل مختلف دسته‌بندی مانند تشخیص هرزنامه (Spam Detection)، پیش‌بینی دیابت، شناسایی سرطان و موارد مشابه استفاده کرد.

انواع رگرسیون لجستیک

در حالت کلی، زمانی که از رگرسیون لجستیک صحبت می‌شود، منظور رگرسیون لجستیک دودویی (Binary Logistic Regression) است که در آن متغیر هدف دارای دو مقدار ممکن است. با این حال، انواع دیگری از متغیرهای هدف نیز وجود دارند که می‌توان آن‌ها را با استفاده از این الگوریتم پیش‌بینی کرد. بر اساس تعداد دسته‌های موجود در متغیر هدف، رگرسیون لجستیک را می‌توان به انواع زیر تقسیم کرد:

دودویی یا دوحالتی (Binary or Binomial)

در این نوع دسته‌بندی، متغیر وابسته تنها دو نوع مقدار ممکن دارد: ۱ یا ۰. برای مثال، این متغیرها می‌توانند نشان‌دهنده موفقیت یا شکست، بله یا خیر، پیروزی یا شکست و موارد مشابه باشند.

چند‌گانه (Multinomial)

در این نوع دسته‌بندی، متغیر وابسته می‌تواند دارای سه یا چند نوع مقدار نامرتبط باشد؛ به این معنا که بین دسته‌ها هیچ ترتیب یا معنای عددی وجود ندارد. برای مثال، این متغیرها ممکن است نمایانگر “نوع A”، “نوع B” یا “نوع C” باشند.

ترتیبی (Ordinal)

در این نوع دسته‌بندی، متغیر وابسته می‌تواند دارای سه یا چند مقدار مرتب‌شده باشد که دارای معنا و اهمیت عددی هستند. برای مثال، این متغیرها ممکن است شامل دسته‌هایی مانند “ضعیف”، “خوب”، “خیلی خوب” و “عالی” باشند که هرکدام می‌توانند نمره‌ای مانند ۰، ۱، ۲ و ۳ داشته باشند.

فرضیات رگرسیون لجستیک

پیش از اجرای الگوریتم رگرسیون لجستیک، باید با چند فرض مهم در مورد این مدل آشنا باشیم. رعایت این موارد برای دستیابی به نتایج دقیق و قابل اعتماد ضروری است:

در رگرسیون لجستیک دودویی (Binary Logistic Regression)، متغیر هدف باید به‌صورت دودویی باشد. به‌عبارت دیگر، فقط دو مقدار ممکن مانند ۱ و ۰ را می‌پذیرد. در این حالت، مقدار ۱ به‌عنوان نتیجه مطلوب (موفقیت یا بله) در نظر گرفته می‌شود.
نباید بین متغیرهای مستقل هم‌خطی چندگانه (Multicollinearity) وجود داشته باشد. این یعنی متغیرهای مستقل باید از یکدیگر مستقل باشند و همبستگی زیادی با هم نداشته باشند.
در مدل باید از متغیرهای معنادار و مرتبط استفاده شود. متغیرهایی که هیچ رابطه‌ای با متغیر هدف ندارند، باید حذف شوند.
برای رگرسیون لجستیک، باید حجم نمونه (Sample Size) کافی و بزرگ در نظر گرفته شود. نمونه‌های بیشتر باعث افزایش دقت مدل و کاهش خطای تخمین خواهند شد.

مدل رگرسیون لجستیک دودویی

ساده‌ترین نوع رگرسیون لجستیک، رگرسیون لجستیک دودویی یا دوجمله‌ای (Binomial) است. در این مدل، متغیر هدف یا وابسته تنها می‌تواند دو مقدار ممکن داشته باشد: ۱ یا ۰. این الگوریتم به ما اجازه می‌دهد تا رابطه‌ای بین چندین متغیر پیش‌بین (Predictor Variables) و یک متغیر هدف دودویی ایجاد کنیم.

در رگرسیون لجستیک، از یک تابع خطی به‌عنوان ورودی یک تابع دیگر استفاده می‌شود. شکل کلی این رابطه به صورت زیر است:

در اینجا $g (z)$ تابع لجستیک یا سیگموید (Sigmoid Function) است که به‌صورت زیر تعریف می‌شود:

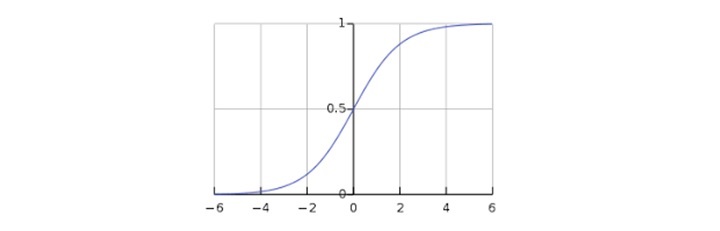
نمودار منحنی سیگموید به ما کمک می‌کند تا درک بهتری از رفتار تابع داشته باشیم. همان‌طور که در شکل مربوطه مشخص است، مقدار خروجی این تابع همواره بین ۰ و ۱ قرار دارد و محور y را در مقدار ۰٫۵ قطع می‌کند.

خروجی تابع فرضیه (Hypothesis Function) را می‌توان به‌صورت یک احتمال تفسیر کرد. اگر مقدار خروجی بین ۰ و ۱ باشد، بیانگر احتمال تعلق به کلاس مثبت است. در پیاده‌سازی ما، اگر خروجی دقیقاً برابر یا بزرگ‌تر از ۰٫۵ باشد، آن را مثبت در نظر می‌گیریم؛ در غیر این صورت، خروجی منفی تلقی می‌شود.

برای سنجش عملکرد مدل، باید تابعی تعریف کنیم که خطای مدل را اندازه‌گیری کند. این تابع که تابع هزینه یا زیان نامیده می‌شود، به‌صورت زیر تعریف می‌شود:

اکنون که تابع هزینه (Loss Function) را تعریف کردیم، هدف اصلی ما کمینه‌سازی مقدار این تابع است. برای دستیابی به این هدف، باید وزن‌ها (Weights) یا ضرایب مدل را به‌درستی تنظیم کنیم. این تنظیم به معنای افزایش یا کاهش تدریجی وزن‌ها با هدف بهبود دقت مدل است.

معادله زیر که مربوط به روش گرادیان نزولی (Gradient Descent) است، نشان می‌دهد که با تغییر پارامترها، مقدار تابع هزینه چگونه تغییر خواهد کرد:

پیاده‌سازی مدل رگرسیون لجستیک دودویی در پایتون

در این بخش، مفهوم رگرسیون لجستیک دودویی را با استفاده از زبان پایتون پیاده‌سازی می‌کنیم. برای این منظور، از دیتاست چند‌متغیره معروفی به نام iris استفاده می‌کنیم. این مجموعه داده شامل سه کلاس است که هر کدام ۵۰ نمونه دارند. اما ما تنها از دو ویژگی اول آن استفاده می‌کنیم. هر کلاس نمایانگر نوعی از گل زنبق (Iris) است.

ابتدا باید کتابخانه‌های موردنیاز را وارد کنیم:

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets

import numpy as np

import matplotlib.pyplot as plt

import seaborn as sns

from sklearn import datasets

سپس دیتاست iris را بارگذاری کرده و متغیرهای ویژگی و هدف را مشخص می‌کنیم:

iris = datasets.load_iris()
X = iris.data[:, :2]
y = (iris.target != 0) * 1

iris = datasets.load_iris()

X = iris.data[:, :2]

y = (iris.target != 0) * 1

در این مرحله، داده‌های آموزشی را به‌صورت نمودار ترسیم می‌کنیم:

plt.figure(figsize=(6, 6))
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='g', label='0')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='y', label='1')
plt.legend();

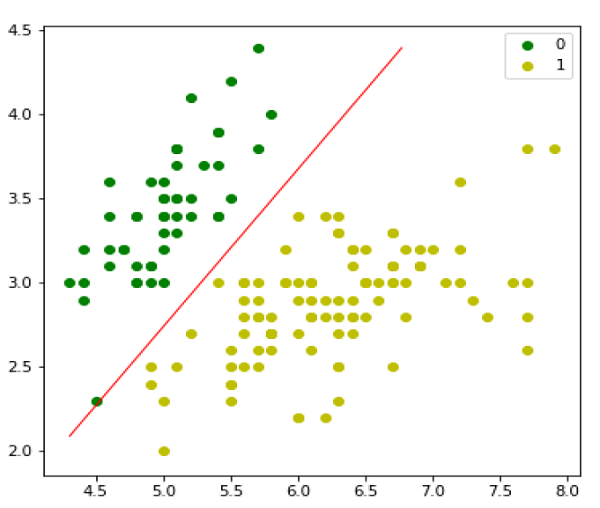
plt.figure(figsize=(6, 6))

plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='g', label='0')

plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='y', label='1')

plt.legend();

اکنون کلاس مربوط به رگرسیون لجستیک را تعریف می‌کنیم. در این کلاس، توابعی مانند تابع سیگموید، تابع هزینه، و گرادیان نزولی پیاده‌سازی می‌شوند:

class LogisticRegression:
   def __init__(self, lr=0.01, num_iter=100000, fit_intercept=True, verbose=False):
      self.lr = lr
      self.num_iter = num_iter
      self.fit_intercept = fit_intercept
      self.verbose = verbose
   def __add_intercept(self, X):
      intercept = np.ones((X.shape[0], 1))
      return np.concatenate((intercept, X), axis=1)
   def __sigmoid(self, z):
      return 1 / (1 + np.exp(-z))
   def __loss(self, h, y):
      return (-y * np.log(h) - (1 - y) * np.log(1 - h)).mean()
   def fit(self, X, y):
      if self.fit_intercept:
         X = self.__add_intercept(X)

class LogisticRegression:

def __init__(self, lr=0.01, num_iter=100000, fit_intercept=True, verbose=False):

self.lr = lr

self.num_iter = num_iter

self.fit_intercept = fit_intercept

self.verbose = verbose

def __add_intercept(self, X):

intercept = np.ones((X.shape[0], 1))

return np.concatenate((intercept, X), axis=1)

def __sigmoid(self, z):

return 1 / (1 + np.exp(-z))

def __loss(self, h, y):

return (-y * np.log(h) - (1 - y) * np.log(1 - h)).mean()

def fit(self, X, y):

if self.fit_intercept:

X = self.__add_intercept(X)

اکنون، وزن‌ها را به صورت زیر مقداردهی اولیه کنید:

self.theta = np.zeros(X.shape[1])
   for i in range(self.num_iter):
      z = np.dot(X, self.theta)
      h = self.__sigmoid(z)
      gradient = np.dot(X.T, (h - y)) / y.size
      self.theta -= self.lr * gradient
      z = np.dot(X, self.theta)
      h = self.__sigmoid(z)
      loss = self.__loss(h, y)
      if(self.verbose ==True and i % 10000 == 0):
         print(f'loss: {loss} \t')

self.theta = np.zeros(X.shape[1])

for i in range(self.num_iter):

z = np.dot(X, self.theta)

h = self.__sigmoid(z)

gradient = np.dot(X.T, (h - y)) / y.size

self.theta -= self.lr * gradient

z = np.dot(X, self.theta)

h = self.__sigmoid(z)

loss = self.__loss(h, y)

if(self.verbose ==True and i % 10000 == 0):

print(f'loss: {loss} \t')

با استفاده از توابع زیر، می‌توان خروجی مدل را به‌صورت احتمال یا به‌صورت کلاس‌های دودویی پیش‌بینی کرد:

def predict_prob(self, X):
   if self.fit_intercept:
      X = self.__add_intercept(X)
   return self.__sigmoid(np.dot(X, self.theta))
def predict(self, X):
   return self.predict_prob(X).round()

def predict_prob(self, X):

if self.fit_intercept:

X = self.__add_intercept(X)

return self.__sigmoid(np.dot(X, self.theta))

def predict(self, X):

return self.predict_prob(X).round()

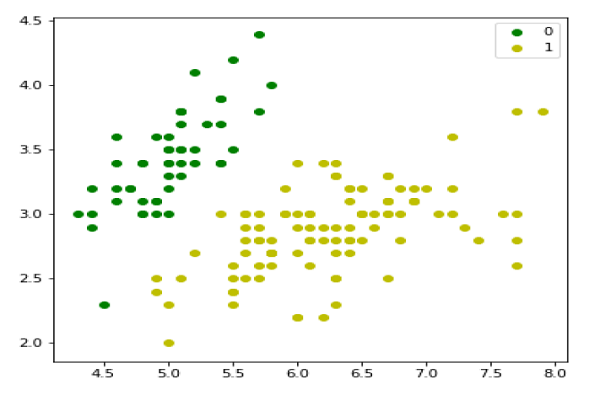
در مرحله بعد، می‌توانیم مدل را ارزیابی کرده و آن را به صورت زیر رسم کنیم:

model = LogisticRegression(lr=0.1, num_iter=300000)
preds = model.predict(X)
(preds == y).mean()

plt.figure(figsize=(10, 6))
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='g', label='0')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='y', label='1')
plt.legend()
x1_min, x1_max = X[:,0].min(), X[:,0].max(),
x2_min, x2_max = X[:,1].min(), X[:,1].max(),
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max), np.linspace(x2_min, x2_max))
grid = np.c_[xx1.ravel(), xx2.ravel()]
probs = model.predict_prob(grid).reshape(xx1.shape)
plt.contour(xx1, xx2, probs, [0.5], linewidths=1, colors='red');

model = LogisticRegression(lr=0.1, num_iter=300000)

preds = model.predict(X)

(preds == y).mean()

plt.figure(figsize=(10, 6))

plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='g', label='0')

plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='y', label='1')

plt.legend()

x1_min, x1_max = X[:,0].min(), X[:,0].max(),

x2_min, x2_max = X[:,1].min(), X[:,1].max(),

xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max), np.linspace(x2_min, x2_max))

grid = np.c_[xx1.ravel(), xx2.ravel()]

probs = model.predict_prob(grid).reshape(xx1.shape)

plt.contour(xx1, xx2, probs, [0.5], linewidths=1, colors='red');

اگر هنوز با مفاهیم اولیه برنامه نویسی آشنا نیستید و می‌خواهید به‌طور اصولی یادگیری پایتون را شروع کنید، بهترین راه شروع، شرکت در آموزش پایتون از صفر است. این دوره به شما کمک می‌کند تا با اصول اولیه پایتون آشنا شوید و به تدریج مهارت‌های لازم برای پیاده‌سازی الگوریتم‌های یادگیری ماشین و پروژه‌های پیچیده را کسب کنید.

مدل رگرسیون لجستیک چندگانه

یکی دیگر از انواع کاربردی رگرسیون لجستیک، رگرسیون لجستیک چندگانه است. در این نوع مدل، متغیر هدف می‌تواند دارای سه یا بیش از سه مقدار نامرتبط (نامرتب) باشد. به‌عبارت دیگر، مقادیر این متغیر فاقد ترتیب عددی یا معنای کمی هستند.

پیاده‌سازی مدل رگرسیون لجستیک چندگانه در پایتون

در این بخش، مدل چندگانه رگرسیون لجستیک را با استفاده از زبان پایتون پیاده‌سازی می‌کنیم. برای این منظور، از مجموعه داده‌ای به نام digits که در کتابخانه sklearn موجود است استفاده خواهیم کرد. این دیتاست شامل تصاویر دیجیتال عددی (رقمی) است.

در ابتدا باید کتابخانه‌های لازم را بارگذاری کنیم:

Import sklearn
from sklearn import datasets
from sklearn import linear_model
from sklearn import metrics
from sklearn.model_selection import train_test_split

Import sklearn

from sklearn import datasets

from sklearn import linear_model

from sklearn import metrics

from sklearn.model_selection import train_test_split

سپس دیتاست digits را بارگذاری می‌کنیم:

digits = datasets.load_digits()

1	digits = datasets.load_digits()

در این مرحله، ویژگی‌ها (X) و متغیر هدف (y) را تعریف می‌کنیم:

X = digits.data
y = digits.target

1 2	X = digits.data y = digits.target

با استفاده از کد زیر، داده‌ها را به دو بخش آموزشی و آزمایشی تقسیم می‌کنیم:

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1)

1	X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1)

اکنون یک شیء از رگرسیون لجستیک به شرح زیر ایجاد کنید:

digreg = linear_model.LogisticRegression()

1	digreg = linear_model.LogisticRegression()

مدل را با استفاده از داده‌های آموزشی آموزش می‌دهیم:

digreg.fit(X_train, y_train)

1	digreg.fit(X_train, y_train)

سپس با استفاده از داده‌های آزمون، پیش‌بینی انجام می‌دهیم:

y_pred = digreg.predict(X_test)

1	y_pred = digreg.predict(X_test)

در نهایت، دقت مدل را محاسبه و چاپ می‌کنیم:

print("Accuracy of Logistic Regression model is:",
metrics.accuracy_score(y_test, y_pred)*100)

1 2	print("Accuracy of Logistic Regression model is:", metrics.accuracy_score(y_test, y_pred)*100)

خروجی

Accuracy of Logistic Regression model is: 95.6884561891516

1	Accuracy of Logistic Regression model is: 95.6884561891516

از خروجی بالا می‌توانیم ببینیم که دقت مدل ما حدود ۹۶ درصد است.

5/5 - (1 امتیاز)

راستی! برای دریافت مطالب جدید در کانال تلگرام یا پیج اینستاگرام سورس باران عضو شوید.

نظرات

برچسب ها: آموزش برنامه نویسی, آموزش پایتون

دوره صفر تا صد آموزش بین المللی لینوکس

انتشار: ۳۱ مرداد ۱۴۰۴