ماشین بردار پشتیبان در یادگیری ماشین (Support Vector Machines یا SVMs) الگوریتمی قدرتمند و در عین حال انعطافپذیر در یادگیری ماشین نظارتشده هستند که برای هر دو مسئله طبقهبندی (classification) و رگرسیون (regression) بهکار میروند. با این حال، معمولاً در مسائل طبقهبندی استفاده میشوند.
نخستین بار در دهه ۱۹۶۰، الگوریتم SVM معرفی شد، اما در دهه ۱۹۹۰ توسعه و بهبود یافت. ماشینهای بردار پشتیبان نسبت به سایر الگوریتمهای یادگیری ماشین، شیوهای منحصربهفرد در پیادهسازی دارند.
امروزه، SVMها بهدلیل توانایی بالا در مدیریت متغیرهای پیوسته و دستهای (categorical)، بسیار محبوب و پرکاربرد هستند.
نحوه عملکرد ماشین بردار پشتیبان (SVM)
هدف اصلی SVM یافتن یک ابرصفحه (Hyperplane) است که بتواند نقاط داده را به درستی به کلاسهای مختلف تقسیم کند. ابرصفحه در فضای دوبعدی یک خط، در فضای سهبعدی یک صفحه، و در فضاهای با ابعاد بالاتر، یک سطح چندبُعدی است.
این ابرصفحه بهگونهای انتخاب میشود که حاشیه (Margin) را بیشینه کند؛ یعنی فاصلهای که بین ابرصفحه و نزدیکترین نقاط از هر کلاس وجود دارد. این نزدیکترین نقاط، بردارهای پشتیبان (Support Vectors) نامیده میشوند.
فاصله بین ابرصفحه و یک نقطه دادهای xx با استفاده از فرمول زیر محاسبه میشود:
|
1 |
distance = (w . x + b) / ||w|| |
در این رابطه:
-
بردار وزن (Weight vector) است؛
-
جمله بایاس (Bias term) است؛
-
||w|| نورم اقلیدسی (Euclidean norm) بردار وزن است.
بردار وزن w عمود بر ابرصفحه است و جهت آن را مشخص میکند، در حالی که جمله بایاس b موقعیت قرارگیری ابرصفحه را تعیین میکند.
یافتن ابرصفحه بهینه از طریق حل یک مسئله بهینهسازی انجام میشود. هدف، بیشینهسازی حاشیه با این شرط است که تمام نقاط دادهای بهدرستی طبقهبندی شوند. به عبارت دیگر، میخواهیم ابرصفحهای پیدا کنیم که فاصله بین کلاسها را بیشینه کند و هیچ نقطهای بهاشتباه در کلاس نادرست قرار نگیرد. این مسئله، یک مسئله بهینهسازی محدب (Convex Optimization Problem) است که با روش برنامهریزی درجه دوم (Quadratic Programming) قابل حل است.
اگر دادهها بهصورت خطی قابل تفکیک نباشند، از تکنیکی به نام ترفند هستهای (Kernel Trick) استفاده میکنیم. در این روش، دادهها به یک فضای با ابعاد بالاتر نگاشت میشوند، جایی که در آن قابل تفکیک شوند. تابع هستهای (Kernel Function) ضرب داخلی بین نگاشت دادهها را محاسبه میکند، بدون اینکه خود نگاشت را انجام دهد. این کار باعث میشود بتوانیم با دادهها در فضای با ابعاد بالاتر کار کنیم، بدون آنکه هزینه محاسباتی بالای نگاشت را بپردازیم.
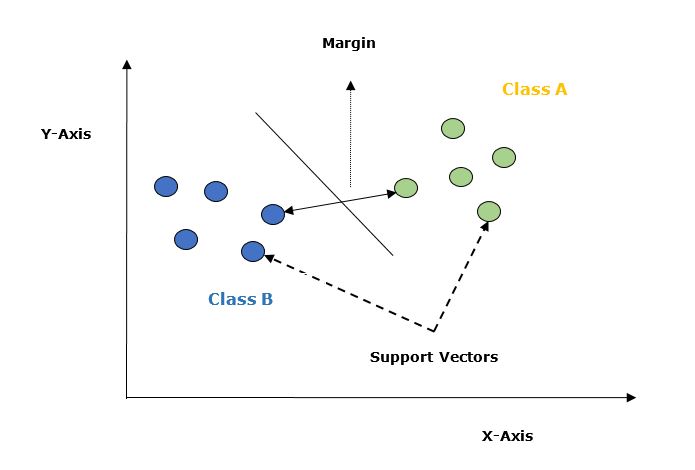
بیایید مفاهیم اصلی SVM را با کمک نمودار زیر بهتر درک کنیم:
مفاهیم کلیدی در SVM
-
بردارهای پشتیبان (Support Vectors): نقاطی از دادهها که نزدیکترین فاصله را به ابرصفحه دارند. ابرصفحه تفکیککننده با توجه به همین نقاط تعیین میشود.
-
ابرصفحه (Hyperplane): همانطور که در نمودار دیده میشود، یک صفحه تصمیمگیری است که فضای دادهها را به بخشهایی تقسیم میکند که هرکدام به یک کلاس تعلق دارند.
-
حاشیه (Margin): فاصله بین دو خطی که نزدیکترین نقاط از دو کلاس مختلف را در بر میگیرند. این فاصله بهصورت عمودی از ابرصفحه تا بردارهای پشتیبان اندازهگیری میشود.
-
حاشیه بزرگ، حاشیه مطلوب و نشانه طبقهبندی خوب است.
-
حاشیه کوچک، کیفیت پایین مدل را نشان میدهد.
-
پیاده سازی SVM با استفاده از پایتون
برای پیاده سازی ماشین بردار پشتیبان (SVM) در زبان پایتون، ابتدا باید کتابخانههای استاندارد مورد نیاز را وارد کنیم:
|
1 2 3 4 |
import numpy as np import matplotlib.pyplot as plt from scipy import stats import seaborn as sns; sns.set() |
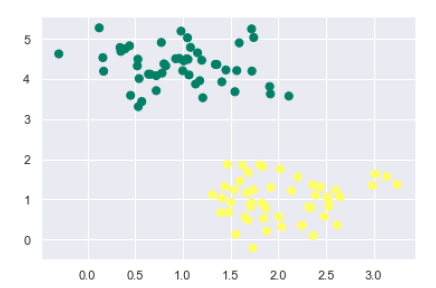
make_blobs در ماژول sklearn.datasets برای ساخت دادهها استفاده میکنیم:|
1 2 3 |
from sklearn.datasets import make_blobs X, y = make_blobs(n_samples=100, centers=2, random_state=0, cluster_std=0.50) plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer'); |
میدانیم که SVM نوعی طبقهبند تبعیضگر (Discriminative Classifier) است؛ یعنی با یافتن یک خط (در فضای دوبعدی) یا یک منیفولد (در فضاهای چندبُعدی)، کلاسها را از یکدیگر جدا میکند.
در ادامه، پیادهسازی آن بر روی دادههای فوق به این صورت خواهد بود:
|
1 2 3 4 5 6 |
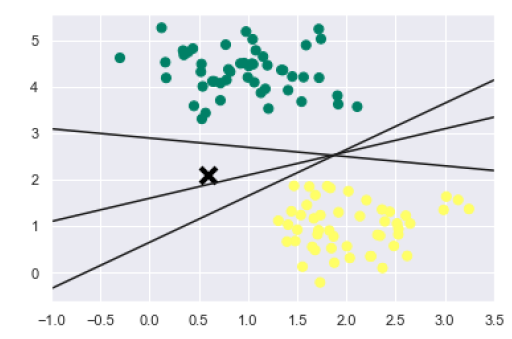
xfit = np.linspace(-1, 3.5) plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer') plt.plot([0.6], [2.1], 'x', color='black', markeredgewidth=4, markersize=12) for m, b in [(1, 0.65), (0.5, 1.6), (-0.2, 2.9)]: plt.plot(xfit, m * xfit + b, '-k') plt.xlim(-1, 3.5); |
ما میتوانیم از خروجی بالا مشاهده کنیم که سه خط مختلف وجود دارند که بهدرستی نقاط دادهای را از یکدیگر جدا میکنند.
همانطور که پیشتر گفته شد، هدف اصلی SVM یافتن ابرصفحهای با بیشترین حاشیه (Maximum Marginal Hyperplane – MMH) است. به جای صرفاً رسم یک خط بین دو کلاس، میتوان برای هر خط، یک حاشیه (margin) با عرض مشخص تا نزدیکترین نقطه رسم کرد. این کار به شکل زیر انجام میشود:
|
1 2 3 4 5 6 7 8 |
xfit = np.linspace(-1, 3.5) plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer') for m, b, d in [(1, 0.65, 0.33), (0.5, 1.6, 0.55), (-0.2, 2.9, 0.2)]: yfit = m * xfit + b plt.plot(xfit, yfit, '-k') plt.fill_between(xfit, yfit - d, yfit + d, edgecolor='none', color='#AAAAAA', alpha=0.4) plt.xlim(-1, 3.5); |
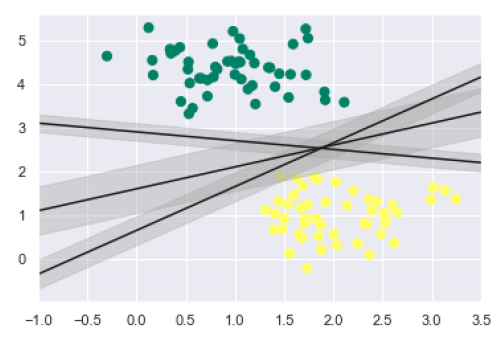
این نمودار بهوضوح نشان میدهد که حاشیه (Margin) در هر مورد چقدر است. اینجا SVM، خطی را انتخاب میکند که بیشترین حاشیه ممکن را داشته باشد؛ بهعبارت دیگر، فاصله بین خط و نزدیکترین نقاط هر کلاس بیشینه باشد.
در مرحله بعد، از کلاس Support Vector Classifier (SVC) در کتابخانه Scikit-Learn برای آموزش مدل SVM روی همین دادهها استفاده میکنیم. در این مثال، ما از کرنل خطی (Linear Kernel) استفاده میکنیم:
|
1 2 3 |
from sklearn.svm import SVC # "Support vector classifier" model = SVC(kernel='linear', C=1E10) model.fit(X, y) |
|
1 2 3 4 |
SVC(C=10000000000.0, cache_size=200, class_weight=None, coef0=0.0, decision_function_shape='ovr', degree=3, gamma='auto_deprecated', kernel='linear', max_iter=-1, probability=False, random_state=None, shrinking=True, tol=0.001, verbose=False) |
ترسیم توابع تصمیم برای مدل SVC دوبُعدی
برای درک بهتر عملکرد مدل آموزشدیده، در ادامه تابعی را تعریف میکنیم که توابع تصمیم (Decision Functions) مدل را روی نمودار رسم میکند:
|
1 2 3 4 5 |
def decision_function(model, ax=None, plot_support=True): if ax is None: ax = plt.gca() xlim = ax.get_xlim() ylim = ax.get_ylim() |
ارزیابی مدل SVM و ترسیم ابرصفحه بهینه
برای ارزیابی مدل و ترسیم خطوط تصمیم (decision boundaries) و حاشیهها (margins)، ابتدا باید یک شبکه دوبُعدی از نقاط مختصات (grid) در فضای داده ایجاد کنیم. این کار بهصورت زیر انجام میشود:
|
1 2 3 4 5 |
x = np.linspace(xlim[0], xlim[1], 30) y = np.linspace(ylim[0], ylim[1], 30) Y, X = np.meshgrid(y, x) xy = np.vstack([X.ravel(), Y.ravel()]).T P = model.decision_function(xy).reshape(X.shape) |
اکنون میتوان مرز تصمیم و خطوط حاشیهای را روی نمودار رسم کرد:
|
1 2 3 |
ax.contour(X, Y, P, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--']) |
در ادامه، بردارهای پشتیبان را نیز با نقاط توخالی روی نمودار مشخص میکنیم:
|
1 2 3 4 5 6 |
if plot_support: ax.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1], s=300, linewidth=1, facecolors='none'); ax.set_xlim(xlim) ax.set_ylim(ylim) |
اکنون میتوانیم کل مدل را بههمراه مرز تصمیم، حاشیهها و بردارهای پشتیبان، بهصورت کامل ترسیم کنیم:
|
1 2 |
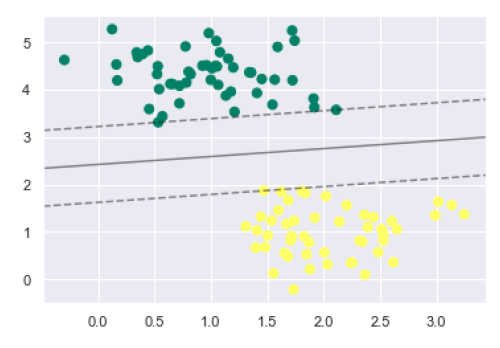
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer') decision_function(model); |
میتوانیم از خروجی بالا ببینیم که طبقه بندی کننده SVM روی داده برازش میشود و حاشیهها را نشان میدهد. خطوط حاشیه با خطچین نمایش داده میشوند و بردارهای پشتیبان عنصرهای کلیدی این برازش هستند. این نقاط خطچین را لمس میکنند.
این نقاطِ بردار پشتیبان در ویژگی (attribute) support_vectors_ طبقهبندی کننده ذخیره میشوند، بهشکل زیر:
|
1 |
model.support_vectors_ |
|
1 2 3 |
array([[0.5323772 , 3.31338909], [2.11114739, 3.57660449], [1.46870582, 1.86947425]]) |
هستهها در SVM
در عمل، الگوریتم SVM معمولاً با استفاده از هسته (Kernel) پیادهسازی میشود. هسته دادههای ورودی را از یک فضای اولیه به شکلی تبدیل میکند که برای طبقهبندی مناسب باشد.
SVM از تکنیکی به نام ترفند هستهای (Kernel Trick) استفاده میکند. در این روش، هسته یک فضای ورودی با ابعاد پایین را به یک فضای با ابعاد بالاتر نگاشت میکند. به زبان ساده، هسته مسائل غیرقابلتفکیک (Non-separable) را با افزودن بُعدهای بیشتر به مسائل قابلتفکیک (Separable) تبدیل میکند.
این ویژگی باعث میشود SVM قدرتمندتر، انعطافپذیرتر و دقیقتر عمل کند. انواع مختلفی از هستهها در SVM مورد استفاده قرار میگیرند که مهمترین آنها عبارتاند از:
هسته خطی (Linear Kernel)
از این هسته میتوان بهعنوان ضرب داخلی (Dot Product) بین هر دو مشاهده استفاده کرد. فرمول هسته خطی به صورت زیر است:
k(x,xi) = sum(x*xi)
از فرمول بالا میتوانیم ببینیم که حاصلضرب بین دو بردار برابر است با مجموع حاصلضرب هر جفت مقدار ورودی.
هسته چندجملهای (Polynomial Kernel)
این هسته شکل عمومیتر هسته خطی است و میتواند فضاهای ورودی منحنی یا غیرخطی را متمایز کند. فرمول هسته چندجملهای به صورت زیر است:
K(x, xi) = 1 + sum(x * xi)^d
در اینجا، d درجه چندجملهای است که باید بهصورت دستی در الگوریتم یادگیری مشخص کنیم.
هسته تابع پایه شعاعی (Radial Basis Function – RBF Kernel)
هسته RBF که بیشتر در طبقهبندیهای SVM استفاده میشود، فضای ورودی را به یک فضای با ابعاد نامحدود نگاشت میکند. فرمول ریاضی آن به صورت زیر است:
K(x,xi) = exp(-gamma * sum((x xi^2))
در اینجا، مقدار γ بین 0 و 1 است. ما باید آن را بهصورت دستی در الگوریتم مشخص کنیم. مقدار پیشفرض مناسب برای γ، عدد 0.1 در نظر گرفته میشود.
همانطور که SVM را برای دادههای خطی قابل تفکیک پیادهسازی کردیم، میتوانیم آن را در Python برای دادههایی که بهصورت خطی قابل تفکیک نیستند نیز پیادهسازی کنیم. این کار با استفاده از هستهها (Kernels) انجام میشود.
مثال
در این مثال، یک دستهبند SVM با استفاده از هستهها (Kernels) ایجاد میکنیم. برای این کار از مجموعه داده Iris موجود در کتابخانه scikit-learn استفاده خواهیم کرد.
ابتدا بسته های مورد نیاز را وارد میکنیم:
|
1 2 3 4 |
import pandas as pd import numpy as np from sklearn import svm, datasets import matplotlib.pyplot as plt |
|
1 |
iris = datasets.load_iris() |
|
1 2 |
X = iris.data[:, :2] y = iris.target |
|
1 2 3 4 5 6 |
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1 y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1 h = (x_max / x_min)/100 xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) X_plot = np.c_[xx.ravel(), yy.ravel()] |
|
1 |
C = 1.0 |
Svc_classifier = svm.SVC(kernel=’linear’, C=C).fit(X, y)
|
1 2 3 4 5 6 7 8 9 10 |
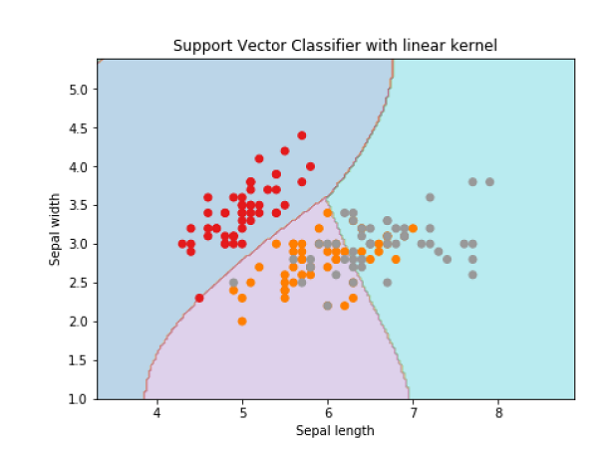
Z = svc_classifier.predict(X_plot) Z = Z.reshape(xx.shape) plt.figure(figsize=(15, 5)) plt.subplot(121) plt.contourf(xx, yy, Z, cmap=plt.cm.tab10, alpha=0.3) plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1) plt.xlabel('Sepal length') plt.ylabel('Sepal width') plt.xlim(xx.min(), xx.max()) plt.title('Support Vector Classifier with linear kernel') |
خروجی
|
1 |
Text(0.5, 1.0, 'Support Vector Classifier with linear kernel') |
برای ایجاد یک دستهبند SVM با هسته RBF، کافی است مقدار پارامتر kernel را از linear به rbf تغییر دهیم:
|
1 2 3 4 5 6 7 8 9 10 11 |
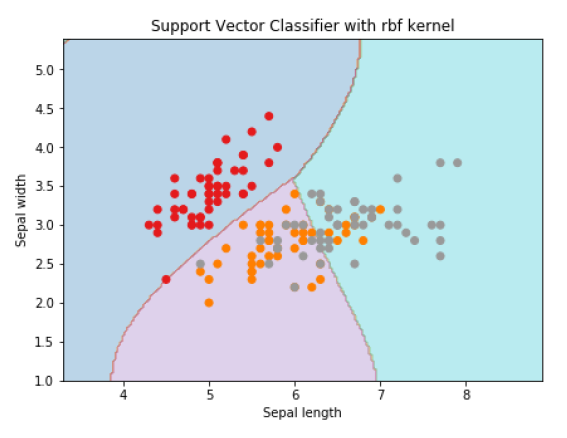
Svc_classifier = svm.SVC(kernel='rbf', gamma ='auto',C=C).fit(X, y) Z = svc_classifier.predict(X_plot) Z = Z.reshape(xx.shape) plt.figure(figsize=(15, 5)) plt.subplot(121) plt.contourf(xx, yy, Z, cmap=plt.cm.tab10, alpha=0.3) plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1) plt.xlabel('Sepal length') plt.ylabel('Sepal width') plt.xlim(xx.min(), xx.max()) plt.title('Support Vector Classifier with rbf kernel') |
خروجی
|
1 |
Text(0.5, 1.0, 'Support Vector Classifier with rbf kernel') |
ما مقدار گاما (gamma) را برابر 'auto' قرار دادیم، اما شما میتوانید بهصورت دستی نیز برای آن مقداری بین ۰ تا ۱ تعیین کنید.
تنظیم پارامترهای SVM
در عمل، الگوریتمهای SVM معمولاً نیاز به تنظیم پارامترها دارند تا بهترین عملکرد را ارائه دهند. مهمترین پارامترهایی که باید تنظیم شوند شامل کرنل (Kernel)، پارامتر منظمسازی C و پارامترهای خاص هر کرنل هستند.
پارامتر کرنل (Kernel) نوع کرنل مورد استفاده را مشخص میکند. رایجترین انواع کرنل شامل خطی (Linear)، چندجملهای (Polynomial)، تابع پایه شعاعی (RBF) و سیگموید (Sigmoid) هستند. کرنل خطی برای دادههای خطی تفکیکپذیر استفاده میشود، در حالی که سایر کرنلها برای دادههای غیرخطی تفکیکناپذیر بهکار میروند.
پارامتر C یا همان پارامتر منظمسازی، میزان موازنه بین بیشینهسازی حاشیه (Margin) و کاهش خطای طبقهبندی را کنترل میکند:
-
اگر مقدار C بزرگ باشد، طبقهبند تلاش میکند خطای طبقهبندی را به حداقل برساند، حتی اگر به قیمت کوچکتر شدن حاشیه باشد.
-
اگر مقدار C کوچک باشد، طبقهبند ترجیح میدهد حاشیه را بزرگتر کند، حتی اگر به معنای خطاهای طبقهبندی بیشتر باشد.
پارامترهای ویژه هر کرنل به نوع کرنل بستگی دارند. بهطور مثال:
-
در کرنل چندجملهای (Polynomial) باید درجه چندجملهای (degree) و ضریب چندجملهای مشخص شوند.
-
در کرنل RBF باید پهنای تابع گاوسی (gamma) تعیین شود.
برای انتخاب بهترین مقادیر این پارامترها، میتوان از روش اعتبارسنجی متقابل (Cross-Validation) استفاده کرد. در این روش، دادهها به چند زیرمجموعه تقسیم میشوند و طبقهبند روی بخشی از دادهها آموزش میبیند و روی بخش باقیمانده آزمایش میشود. این فرآیند کمک میکند عملکرد مدل روی بخشهای مختلف داده ارزیابی شود و در نهایت بهترین مجموعه پارامترها انتخاب گردد.
مثال
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
from sklearn.model_selection import GridSearchCV # define the parameter grid param_grid = { 'C': [0.1, 1, 10, 100], 'kernel': ['linear', 'poly', 'rbf', 'sigmoid'], 'degree': [2, 3, 4], 'coef0': [0.0, 0.1, 0.5], 'gamma': ['scale', 'auto'] } # create an SVM classifier svm = SVC() # perform grid search to find the best set of parameters grid_search = GridSearchCV(svm, param_grid, cv=5) grid_search.fit(X_train, y_train) # print the best set of parameters and their accuracy print("Best parameters:", grid_search.best_params_) print("Best accuracy:", grid_search.best_score_) |
ما با وارد کردن ماژول GridSearchCV از کتابخانه Scikit-learn شروع میکنیم. این ابزار برای انجام جستجوی شبکهای (Grid Search) روی مجموعهای از پارامترها بهکار میرود.
ابتدا یک شبکه پارامتر (parameter grid) تعریف میکنیم که شامل مقادیر مختلف هر پارامتری است که میخواهیم آن را تنظیم (tune) کنیم.
سپس یک طبقهبند SVM با استفاده از SVC() ایجاد کرده و آن را به همراه شبکه پارامتر و تعداد foldهای اعتبارسنجی متقابل (cv=5) به GridSearchCV میدهیم. بعد از آن با فراخوانی grid_search.fit(X_train, y_train)، جستجوی شبکهای آغاز میشود.
پس از تکمیل جستجو، میتوانیم بهترین مجموعه پارامترها و همچنین بهترین دقت مدل را با استفاده از ویژگیهای زیر چاپ کنیم:
-
grid_search.best_params_→ بهترین مجموعه پارامترها -
grid_search.best_score_→ بهترین دقت حاصلشده
خروجی
پس از اجرای برنامه، خروجی به صورت زیر خواهد بود:
|
1 2 |
Best parameters: {'C': 0.1, 'coef0': 0.5, 'degree': 3, 'gamma': 'scale', 'kernel': 'poly'} Best accuracy: 0.975 |
این نتایج نشان میدهند که بهترین مجموعه پارامترهایی که توسط Grid Search پیدا شدهاند به صورت زیر است:
-
C = 0.1
-
coef0 = 0.5
-
degree = 3
-
gamma = ‘scale’
-
kernel = ‘poly’
و دقت بهدستآمده روی دادههای آموزشی برابر با ۹۷.۵٪ بوده است.
اکنون میتوانیم از این مجموعه پارامترها برای ایجاد یک طبقهبند جدید SVM استفاده کرده و عملکرد آن را روی دادههای تست ارزیابی کنیم.
مزایا و معایب طبقهبندهای SVM
مزایای طبقهبندهای SVM
-
طبقهبندهای SVM دقت بالایی دارند و عملکرد خوبی در فضای با ابعاد بالا ارائه میکنند.
-
این طبقهبندها عمدتاً از زیرمجموعهای از نقاط آموزشی (support vectors) استفاده میکنند، بنابراین در نتیجه حافظه بسیار کمی مصرف میکنند.
معایب طبقهبندهای SVM
-
زمان آموزش آنها بالا است، بنابراین در عمل برای دادههای بزرگ مناسب نیستند.
-
یکی دیگر از معایب این است که طبقهبندهای SVM با کلاسهای همپوشان به خوبی عمل نمیکنند.
اگر هنوز با مفاهیم اولیه برنامه نویسی آشنا نیستید و میخواهید بهطور اصولی یادگیری پایتون را شروع کنید، بهترین راه شروع، شرکت در آموزش پایتون از صفر است. این دوره به شما کمک میکند تا با اصول اولیه پایتون آشنا شوید و به تدریج مهارتهای لازم برای پیادهسازی الگوریتمهای یادگیری ماشین و پروژههای پیچیده را کسب کنید.
راستی! برای دریافت مطالب جدید در کانال تلگرام یا پیج اینستاگرام سورس باران عضو شوید.
- انتشار: ۱ شهریور ۱۴۰۴
دسته بندی موضوعات
- آموزش ارز دیجیتال
- آموزش برنامه نویسی
- آموزش متنی برنامه نویسی
- اطلاعیه و سایر مطالب
- پروژه برنامه نویسی
- دوره های تخصصی برنامه نویسی
- رپورتاژ
- فیلم های آموزشی
- ++C
- ADO.NET
- Adobe Flash
- Ajax
- AngularJS
- apache
- ARM
- Asp.Net
- ASP.NET MVC
- AVR
- Bootstrap
- CCNA
- CCNP
- CMD
- CSS
- Dreameaver
- EntityFramework
- HTML
- IOS
- jquery
- Linq
- Mysql
- Oracle
- PHP
- PHPMyAdmin
- Rational Rose
- silver light
- SQL Server
- Stimulsoft Reports
- Telerik
- UML
- VB.NET&VB6
- WPF
- Xml
- آموزش های پروژه محور
- اتوکد
- الگوریتم تقریبی
- امنیت
- اندروید
- اندروید استودیو
- بک ترک
- بیسیک فور اندروید
- پایتون
- جاوا
- جاوا اسکریپت
- جوملا
- دلفی
- دوره آموزش Go
- دوره های رایگان پیشنهادی
- زامارین
- سئو
- ساخت CMS
- سی شارپ
- شبکه و مجازی سازی
- طراحی الگوریتم
- طراحی بازی
- طراحی وب
- فتوشاپ
- فریم ورک codeigniter
- فلاتر
- کانستراکت
- کریستال ریپورت
- لاراول
- معماری کامپیوتر
- مهندسی اینترنت
- هوش مصنوعی
- یونیتی
- کتاب های آموزشی
- Android
- ASP.NET
- AVR
- LINQ
- php
- Workflow
- اچ تی ام ال
- بانک اطلاعاتی
- برنامه نویسی سوکت
- برنامه نویسی موبایل
- پاسکال
- پایان نامه
- پایتون
- جاوا
- جاوا اسکریپت
- جی کوئری
- داده کاوی
- دلفی
- رباتیک
- سئو
- سایر کتاب ها
- سخت افزار
- سی اس اس
- سی پلاس پلاس
- سی شارپ
- طراحی الگوریتم
- فتوشاپ
- مقاله
- مهندسی نرم افزار
- هک و امنیت
- هوش مصنوعی
- ویژوال بیسیک
- نرم افزار و ابزار برنامه نویسی
- وردپرس