تورنادو کش (Tornado Cash) یک میکسر رمزارزی مبتنی بر قرارداد هوشمند است. کاربران با استفاده از این ابزار میتوانند رمزارز را از یک آدرس واریز و از آدرس دیگری برداشت کنند. این روش هیچ ارتباط قابل ردیابی بین دو آدرس ایجاد نمیکند.
تورنادو کش (Tornado Cash) را میتوان یکی از برجستهترین نمونههای کاربرد فناوری اثبات دانش صفر (Zero-Knowledge Proofs) در قراردادهای هوشمند دانست. در این مقاله، عملکرد آن را با دقت و در سطحی فنی بررسی میکنیم. این بررسی به گونهای انجام میشود که هر برنامه نویس بتواند این ساختار را بهصورت کامل بازسازی کند.
برای درک این مقاله، لازم است خواننده با نحوه کار درخت های مرکل (Merkle Trees) آشنا باشد. همچنین باید مفهوم غیرقابل بازگشت بودن هش های رمزنگاری شده را بداند. علاوه بر این، تسلط نسبی به زبان برنامه نویسی سالیدیتی ضروری است؛ زیرا در ادامه بخشهایی از کد منبع Tornado Cash را بررسی میکنیم.
هشدار درباره تورنادو کش (Tornado Cash): هک شدن
در تاریخ ۲۷ می، قراردادهای حاکمیتی Tornado Cash (که با قراردادهایی که در این مقاله بررسی میکنیم متفاوت هستند) مورد حمله قرار گرفتند. مهاجم با ثبت یک پیشنهاد مخرب موفق شد اکثریت توکن های رای گیری مبتنی بر ERC20 را بهدست بگیرد و کنترل سیستم حاکمیتی را بهطور موقت تصاحب کند.
پس از این اتفاق، مهاجم بخش زیادی از کنترل را به جامعه بازگرداند و تنها بخش کوچکی از آن را برای خود نگه داشت.
اثبات دانش صفر چگونه کار میکند؟ (برای برنامهنویسانی که از ریاضی متنفرند)
برای درک عملکرد تورنادو کش (Tornado Cash)، نیازی نیست که الگوریتمهای اثبات دانش صفر (Zero Knowledge Proofs) را بشناسید. اما باید بدانید این نوع اثبات ها چگونه کار میکنند.
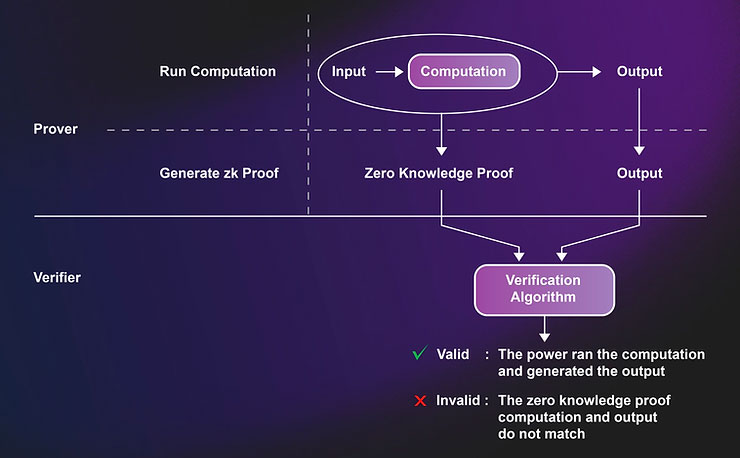
برخلاف نامشان و بسیاری از مثالهای رایج، اثباتهای دانش صفر بهجای اثبات آگاهی از یک حقیقت، درستی انجام یک محاسبه را اثبات میکنند. این سیستمها خودشان محاسبه را انجام نمیدهند. بلکه از سه جزء تشکیل شدهاند: یک محاسبه توافقشده، مدرکی که نشان دهد این محاسبه انجام شده، و نتیجه آن محاسبه. سیستم بررسی میکند آیا طرف اثباتکننده واقعاً محاسبه را اجرا کرده و به این نتیجه رسیده است یا نه.
بخش «دانش صفر» زمانی فعال میشود که این مدرک بهشکلی ارائه شود که هیچ اطلاعاتی درباره ورودیهای اصلی فاش نکند.
بهعنوان مثال، میتوانید نشان دهید که عوامل اول یک عدد را میدانید، بدون آنکه آن عوامل را فاش کنید. این کار با استفاده از الگوریتم RSA امکانپذیر است. الگوریتم RSA بهتنهایی نمیگوید “من دو عدد مخفی را میدانم”، بلکه اثبات میکند که شما این دو عدد را در ذهن خود ضرب کردهاید و حاصل را که همان عدد عمومی است، بهدرستی بهدست آوردهاید.
درواقع رمزنگاری RSA را میتوان یک نمونه خاص از اثباتهای دانش صفر در نظر گرفت. در RSA، شما نشان میدهید که دو عدد اول مخفی را در اختیار دارید که حاصل ضرب آنها کلید عمومی شما را تولید میکند. در دنیای دانش صفر، همین ایده ضرب مخفی را به محاسبات دلخواه تعمیم میدهیم. این محاسبات میتوانند شامل عملیاتهای ریاضی ساده یا شرطهای منطقی باشند.
زمانی که بتوانیم این نوع اثباتها را برای عملیات پایه پیادهسازی کنیم، قادر خواهیم بود اثباتهایی بسیار پیچیدهتر بسازیم. برای مثال میتوانیم اثبات کنیم که تصویر معکوس یک هش را میدانیم، یا ریشه یک درخت مرکل را درست محاسبه کردهایم، یا حتی کل یک ماشین مجازی را با موفقیت اجرا کردهایم.
نکتهای دیگر درباره دانش صفر
در یک سیستم دانش صفر، فرآیند تأیید اصلاً محاسبه را انجام نمیدهد. این سیستم فقط بررسی میکند که آیا فرد اثباتکننده واقعاً محاسبه را انجام داده و خروجی ادعاشده را تولید کرده است یا نه.
و اما یک نتیجهگیری مهم دیگر: برای تولید اثبات دانش صفر از یک محاسبه، باید ابتدا آن محاسبه را بهطور کامل انجام دهید. البته این شرط فقط برای تولید اثبات لازم است، نه برای تأیید آن.
این موضوع کاملاً منطقی است. مگر میتوان ثابت کرد که تصویر معکوس (Preimage) یک تابع هش را میدانید، بدون آنکه واقعاً آن تصویر را هش کرده باشید؟ بنابراین، اثباتکننده باید محاسبه را خودش انجام دهد و سپس با استفاده از داده های کمکی که همان اثبات (Proof) نام دارد، نشان دهد که محاسبه را بهدرستی انجام داده است.
بهطور مشابه، وقتی شما یک امضای RSA را اعتبارسنجی میکنید، لازم نیست عوامل اول کلید خصوصی طرف مقابل را ضرب کنید تا کلید عمومیاش را بسازید. این کار کل منطق رمزنگاری را زیر سوال میبرد. در عوض، یک الگوریتم مستقل وجود دارد که امضا را با پیام بررسی میکند تا مطمئن شود همهچیز درست است.
بنابراین، مفهوم محاسبه در سیستم دانش صفر به شکل زیر تعریف میشود:
|
1 |
verifier_algorithm(proof, computation, public_output) == true |
در زمینه RSA، میتوان کلید عمومی را نتیجه آن محاسبه دانست. پس در این صورت، امضا و پیام نقش اثبات دانش صفر را بازی میکنند.
در چنین ساختاری، خود محاسبه و خروجی آن عمومی هستند. همه میپذیرند که از یک تابع هش مشخص استفاده شده و خروجی معینی بهدست آمده است. اثبات، ورودی آن تابع را مخفی نگه میدارد و فقط نشان میدهد که محاسبه واقعاً انجام شده و خروجی درست بهدست آمده است.
تفاوت اساسی در مرحله تأیید
وقتی فقط به اثبات دسترسی داشته باشیم، تأییدکننده نمیتواند خروجی عمومی (public_output) را محاسبه کند. مرحله تأیید اصلاً محاسبهای انجام نمیدهد. این مرحله فقط بررسی میکند که آیا محاسبه ادعاشده واقعاً انجام شده و با استفاده از آن اثبات، خروجی مورد نظر بهدست آمده است یا نه.
در این مقاله قصد نداریم الگوریتمهای دانش صفر را آموزش دهیم. اما اگر بتوانید بپذیرید که با استفاده از یک اثبات میتوان انجامشدن یک محاسبه را ثابت کرد، بدون آنکه خودمان آن محاسبه را انجام دهیم، ادامه مسیر برایتان روشن خواهد بود.
تراکنش های ناشناس در رمزارزها چگونه عمل میکنند: مفهوم اختلاط (Mixing)
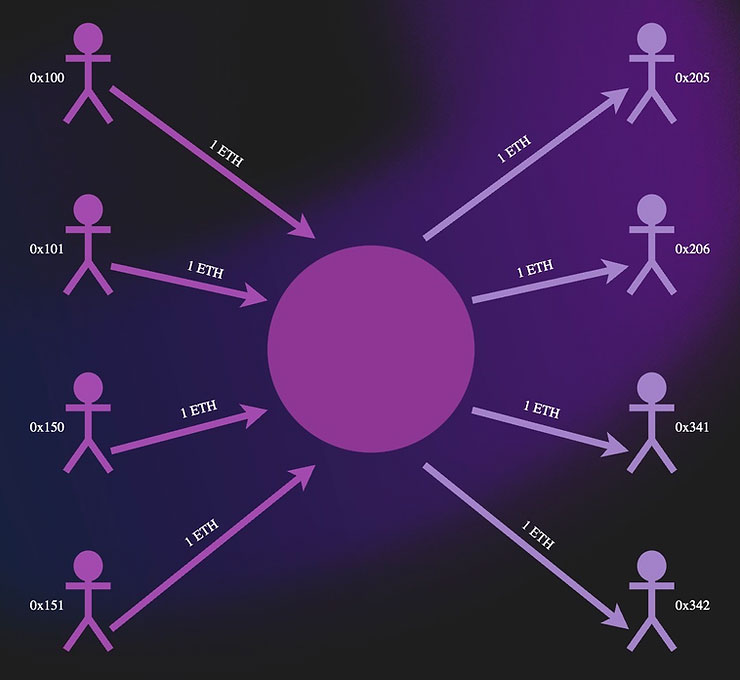
اساس کار تورنادو کش (Tornado Cash) برای ناشناسسازی تراکنش ها، استفاده از تکنیکی به نام اختلاط (Mixing) است؛ روشی که شباهت زیادی به مکانیزم رمزارزهای ناشناس مانند Monero دارد. در این فرآیند، چندین کاربر رمزارز خود را به یک آدرس مشخص ارسال میکنند. این واریزیها در کنار هم “مخلوط” میشوند، بهگونهای که در مرحله برداشت، نمیتوان تشخیص داد کدام برداشت متعلق به کدام واریز بوده است.
فرض کنید ۱۰۰ نفر هرکدام یک اسکناس یک دلاری را داخل یک جعبه بیاندازند. یک روز بعد، ۱۰۰ نفر دیگر از راه میرسند و هرکدام یک اسکناس یک دلاری از همان جعبه برمیدارند. در چنین شرایطی، هیچکس نمیتواند تشخیص دهد که هر اسکناس دقیقاً از طرف چه کسی ارسال شده یا قرار بوده به چه کسی برسد.
اما این روش یک مشکل بدیهی دارد: اگر هرکسی بتواند بدون محدودیت پولی را از آن جعبه بردارد، کل موجودی خیلی سریع به سرقت میرود. از طرف دیگر، اگر بخواهیم اطلاعاتی (متادیتا) باقی بگذاریم تا مشخص شود چه کسی مجاز به برداشت است، همین اطلاعات ممکن است هویت ارسالکننده را فاش کند و ناشناسبودن سیستم را از بین ببرد.
Mixing هیچگاه نمیتواند کاملاً خصوصی باشد
وقتی شما مقداری اتر (Ether) به تورنادو کش (Tornado Cash) ارسال میکنید، این تراکنش کاملاً عمومی است. همچنین زمانی که از Tornado Cash برداشت میکنید، آن عملیات نیز کاملاً در بلاکچین قابل مشاهده است. آنچه عمومی نیست، ارتباط بین آدرس واریزکننده و آدرس برداشتکننده است. البته به شرط آنکه تعداد کافی کاربر دیگر نیز واریز و برداشت انجام داده باشند.
در واقع، تنها چیزی که دیگران میتوانند درباره یک آدرس بفهمند این است که «این آدرس، اتر خود را از Tornado Cash دریافت کرده» یا «این آدرس، اتر را به Tornado Cash واریز کرده است». اما زمانی که یک آدرس از تورنادو کش (Tornado Cash) برداشت میکند، هیچکس نمیتواند تشخیص دهد که این برداشت دقیقاً مربوط به کدام واریز بوده است.
تورنادو کش (Tornado Cash) بدون دانش صفر: بررسی ساده با چند اثبات پیشتصویر هش
فرض کنیم فعلاً نخواهیم از مکانیزم دانش صفر (Zero Knowledge) استفاده کنیم و بخواهیم مسئله را با روش سادهتری حل کنیم. کاربر هنگام واریز اتر به قرارداد هوشمند، دو عدد محرمانه تولید میکند. سپس این دو عدد را بههم متصل میکند و هش حاصل از آن را روی بلاکچین ثبت میکند. (در ادامه توضیح میدهیم چرا از دو عدد استفاده شده، نه یکی.)
وقتی چند کاربر واریز انجام میدهند، مجموعهای از هش های عمومی در قرارداد ذخیره میشود، بدون اینکه کسی بداند این هش ها دقیقاً از چه ورودیهایی ساخته شدهاند. در مرحله برداشت، کاربر باید «ورودی هش (preimage)» مربوط به یکی از این هش ها را فاش کند تا بتواند رمزارز خود را برداشت کند.
اما این روش یک ایراد جدی دارد: برداشتکننده فقط در صورتی میتواند هش درست را ارائه دهد که واریزکننده این اطلاعات را خارج از زنجیره (off-chain) به او منتقل کرده باشد. این موضوع مستقیماً حریم خصوصی را از بین میبرد و هدف کل پروژه را نقض میکند.
ساختار اثبات دانش صفر و مشکل مقیاس پذیری
اگر برداشتکننده بتواند بدون فاشکردن اینکه به کدام هش مربوط است و بدون لو دادن ورودی هش (preimage)، ثابت کند که آن را میداند، ما یک سیستم اختلاط رمزارزی کاملاً کارآمد خواهیم داشت.
یک راه ساده برای انجام این کار این است که مجموعهای از بررسیها را پشت سر هم اجرا کنیم:
|
1 2 3 4 5 6 |
zkproof_preimage_is_valid(proof, hash_{1}) OR zkproof_preimage_is_valid(proof, hash_{2}) OR zkproof_preimage_is_valid(proof, hash_{3}) OR ... zkproof_preimage_is_valid(proof, hash_{n-1}) OR zkproof_preimage_is_valid(proof, hash_{n}) |
در اینجا تأییدکننده (verifier) خودش محاسبهای انجام نمیدهد. فقط بررسی میکند که آیا اثباتکننده (prover) چنین الگوریتمی را اجرا کرده و نتیجه آن true بوده یا نه. این مقدار true فقط در صورتی تولید میشود که اثباتکننده واقعاً ورودی هش (preimage) یکی از مقادیر را بداند.
نکته مهم اینجاست: همه هش های واریز عمومی هستند. آنچه مخفی میماند، این است که برداشتکننده ورودی کدام هش را میداند.
اما این روش یک مشکل مهم دارد. اگر تعداد واریزها زیاد شود، این حلقه منطقی بسیار بزرگ و پرهزینه میشود. بنابراین، ما به ساختار دادهای نیاز داریم که بتواند حجم زیادی از هشها را بهصورت فشرده ذخیره کند.
و خوشبختانه چنین ساختاری وجود دارد: درخت مرکل (Merkle Tree).
استفاده از درخت مرکل برای ذخیره سازی حجم زیادی از هش ها
بهجای اینکه در یک حلقه بزرگ همه هش ها را بررسی کنیم، میتوانیم دو جمله سادهتر و مؤثرتر بگوییم:
۱. «من ورودی هش (preimage) یکی از هشها را میدانم»
۲. «این هش درون درخت مرکل قرار دارد»
این دو جمله، همان چیزی را میرسانند که در روش قبلی میگفتیم: «من ورودی یکی از این هش ها را میدانم»؛ اما این بار با روشی بسیار بهینه تر.
مزیت اصلی درخت مرکل در این است که اثبات عضویت در آن (Merkle proof) در اندازه لگاریتمی نسبت به تعداد برگ های درخت انجام میشود. در مقایسه با حلقههای بزرگ و پرهزینه قبلی، این ساختار بهشدت کارآمدتر است.
در هنگام واریز رمزارز، کاربر دو عدد محرمانه تولید میکند، آنها را بههم میچسباند، هش میگیرد و آن هش را بهعنوان یک برگ در درخت مرکل ذخیره میکند.
اتصال ناشناس برداشتکننده به درخت مرکل با کمک دانش صفر
در زمان برداشت، کاربر باید ابتدا ورودی هش (preimage) یکی از برگ های درخت را ارائه دهد و سپس با استفاده از یک Merkle proof ثابت کند که این برگ واقعاً در ساختار درخت قرار دارد.
در حالت عادی، این روند باعث میشود ارتباطی مستقیم بین واریزکننده و برداشتکننده ایجاد شود. اما اگر بتوانیم هم Merkle proof و هم ورودی هش برگ را بهصورت دانش صفر (Zero Knowledge) اثبات کنیم، این پیوند کاملاً از بین میرود.
با استفاده از دانش صفر، میتوانیم ثابت کنیم که یک Merkle proof معتبر بر اساس ریشه عمومی درخت مرکل ساخته شده و همچنین نشان دهیم که ورودی هش مربوط به برگ نیز معتبر است، بدون اینکه هیچکدام از این داده ها را آشکار کنیم.
نکته مهم امنیتی اینجاست: اینکه فقط اثبات کنیم Merkle proof معتبر بوده کافی نیست. برداشتکننده باید علاوه بر آن، دانش خودش از ورودی هش برگ (preimage of the leaf) را هم بهصورت دانش صفر ثابت کند.
تمام برگهای درخت مرکل بهصورت عمومی در دسترس هستند. هر زمان که کاربری رمزارز واریز میکند، هش مربوط به دو عدد محرمانهاش را منتشر میکند و آن هش در درخت ذخیره میشود. چون ساختار کامل درخت مرکل عمومی است، هرکسی میتواند برای هر برگ یک Merkle proof بسازد. به همین دلیل است که ما باید اثبات کنیم دانش واقعی پشت یکی از این برگها را داریم، نه صرفاً اینکه بتوانیم یک proof تولید کنیم.
اثبات وجود برگ در درخت بهتنهایی کافی نیست
اگر کاربر فقط ثابت کند که یک برگ خاص در درخت مرکل قرار دارد، این کار بهتنهایی مانع جعل اثبات و دزدی نمیشود. زیرا هر کسی میتواند برای برگهای عمومی Merkle proof بسازد.
بنابراین برداشتکننده باید یک قدم فراتر برود: او باید نشان دهد که ورودی هش (preimage) مربوط به آن برگ را میشناسد، بدون آنکه خودِ برگ یا آن ورودیها را فاش کند.
یادتان باشد که هر برگ درخت مرکل هش شده دو عدد محرمانه است. یعنی:
|
1 |
leaf = hash(secret1 + secret2) |
_commitment دقیقاً همین برگ است. هنگام واریز، کاربر این مقدار را ارسال میکند:|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
/** @dev Deposit funds into the contract. The caller must send (for ETH) or approve (for ERC20) value equal to or `denomination` of this instance. @param _commitment the note commitment, which is PedersenHash(nullifier + secret) **/ function deposit(bytes32 _commitment) external payable nonReentrant { require(!commitments[_commitment], "The commitment has been submitted"); uint32 insertedIndex = _insert(_commitment); commitments[_commitment] = true; _processDeposit(); emit Deposit(_commitment, insertedIndex, block.timestamp); } |
اثبات ترکیبی: Merkle proof و دانش preimage در قالب zk-proof
وقتی کاربر قصد برداشت دارد، باید نشان دهد که این محاسبه را انجام داده است:
|
1 |
processMerkleProof(merkleProof, hash(secret1 + secret2)) == merkleRoot |
تابع processMerkleProof، یک Merkle proof و یک برگ را دریافت میکند و بررسی میکند آیا با ریشه مرکل عمومی مطابقت دارد یا نه.
در این سناریو، تأییدکننده همان قرارداد هوشمند تورنادو کش (Tornado Cash) است. این قرارداد فقط زمانی رمزارز را آزاد میکند که یک اثبات معتبر دریافت کند. اثباتکننده هم برداشتکنندهای است که میتواند نشان دهد یکی از برگها را خودش تولید کرده است — یعنی تنها کسی است که ورودی هش آن برگ را میداند.
در عمل، برداشت فقط زمانی ممکن است که برداشتکننده همان کسی باشد که قبلاً واریز کرده، چون فقط اوست که به آن دو عدد محرمانه دسترسی دارد. البته برای حفظ حریم خصوصی، او باید برداشت را با یک آدرس کاملاً متفاوت و بدون ارتباط با آدرس واریزی انجام دهد.
در نهایت، برداشتکننده این محاسبه را واقعاً انجام میدهد (تولید هش برگ و Merkle proof)، سپس یک اثبات دانش صفر (zk-proof) تولید میکند که نشان دهد این عملیات را بهدرستی انجام داده است.
او این zk-proof را به قرارداد هوشمند ارائه میدهد. در این فرآیند، خود مقادیر merkleProof و {secret1, secret2} مخفی میمانند. اما قرارداد هوشمند با استفاده از این اثبات، بررسی میکند که برداشتکننده واقعاً این محاسبه را انجام داده و برگ و ریشه مرکل معتبر تولید شدهاند، بدون اینکه لازم باشد هیچکدام از اطلاعات محرمانه فاش شود.
خلاصه مراحل فرآیند در تورنادو کش (Tornado Cash)
مرحله واریز (Depositor)
کاربر واریزکننده اقدامات زیر را انجام میدهد:
-
دو عدد محرمانه تولید میکند.
-
این دو عدد را بههم متصل کرده و از آنها یک هش تعهد (commitment hash) میسازد.
-
هش تعهد را بهعنوان ورودی به قرارداد ارسال میکند.
-
رمزارز موردنظر را به قرارداد Tornado Cash منتقل میکند.
عملکرد Tornado Cash در مرحله واریز
در هنگام واریز، قرارداد هوشمند Tornado Cash:
-
هش تعهد را بهعنوان یک برگ در درخت مرکل (Merkle Tree) ذخیره میکند.
مرحله برداشت (Withdrawer)
کاربر برداشتکننده، که باید همان فردی باشد که اطلاعات محرمانه را دارد، اقدامات زیر را انجام میدهد:
-
یک Merkle proof معتبر برای اثبات عضویت برگ در درخت ایجاد میکند.
-
دوباره هش تعهد را از همان دو عدد محرمانه تولید میکند.
-
یک اثبات دانش صفر (zk-proof) برای این محاسبات میسازد، بدون آنکه مقادیر واقعی را افشا کند.
-
این اثبات را به قرارداد Tornado Cash ارسال میکند.
عملکرد Tornado Cash در مرحله برداشت
در هنگام برداشت، قرارداد هوشمند Tornado Cash:
-
اثبات ارسالشده را با استفاده از ریشه مرکل عمومی (Merkle root) بررسی میکند.
-
در صورت اعتبارسنجی موفق، رمزارز را به برداشتکننده انتقال میدهد.
جلوگیری از برداشت چندباره
طرحی که در بخش قبل توضیح دادیم، یک ایراد مهم دارد: چه چیزی مانع از این میشود که کاربر چند بار برداشت انجام دهد؟
بهنظر میرسد برای جلوگیری از این مسئله، باید برگ مربوط به واریز را از درخت مرکل حذف کنیم تا مشخص شود آن واریز برداشت شده است. اما این کار بلافاصله فاش میکند که کدام برگ به کدام کاربر تعلق دارد. و این یعنی از بین رفتن کامل حریم خصوصی!
تورنادو کش (Tornado Cash) این مشکل را با یک راهکار بسیار هوشمندانه حل میکند:
هیچوقت برگها را از درخت مرکل حذف نمیکند.
وقتی یک هش تعهد (commitment hash) به درخت مرکل اضافه شد، برای همیشه در آن باقی میماند.
پس چطور جلوی برداشت دوباره گرفته میشود؟
قرارداد هوشمند Tornado Cash از یک مکانیزم بهنام nullifier scheme استفاده میکند. این روش یکی از تکنیکهای رایج در پروتکلهای مبتنی بر دانش صفر (Zero Knowledge) است. در بخش بعدی، دقیقتر بررسی میکنیم که nullifier چیست و چگونه مانع از برداشت تکراری میشود، بدون آنکه هویت کاربر یا محل واریز فاش شود.
جلوگیری از برداشت تکراری با Nullifier Hash
در زمان برداشت، کاربر باید موارد زیر را به قرارداد ارائه دهد:
-
هش nullifier بهصورت عمومی (
nullifierHash) -
اثباتی دانش صفر (zk-proof) که نشان دهد واقعاً این هش از ترکیب nullifier و secret ساخته شده است
قرارداد هوشمند با استفاده از الگوریتم دانش صفر بررسی میکند که آیا کاربر واقعاً ورودی هش nullifier را میداند یا نه. بدون اینکه این مقدار را فاش کند.
سپس، مقدار nullifierHash در یک mapping ثبت میشود. این کار تضمین میکند که هر nullifier فقط یک بار استفاده شود و برداشت تکراری غیرممکن باشد.
چرا فقط یکی از مقادیر را منتشر میکنیم؟
اگر کاربر هر دو عدد محرمانه (nullifier و secret) را فاش میکرد، بلافاصله میشد تشخیص داد کدام برگ از درخت مرکل مربوط به اوست. این اتفاق حریم خصوصی را کاملاً از بین میبرد.
اما اگر فقط nullifier را بهصورت عمومی منتشر کنیم و مقدار دوم (secret) را مخفی نگه داریم، دیگر نمیتوان تشخیص داد این nullifier متعلق به کدام برگ است. در نتیجه ناشناسبودن سیستم حفظ میشود.
نقش دانش صفر در این فرآیند
به یاد داشته باشید، سیستم دانش صفر نمیتواند nullifier را از روی secret محاسبه کند. تنها کاری که میتواند انجام دهد، این است که بررسی کند آیا خروجی هش، محاسبه و اثبات همگی با هم سازگار هستند یا نه.
به همین دلیل کاربر باید nullifierHash را بهصورت عمومی ارائه دهد و بهکمک zk-proof اثبات کند که این مقدار از روی یک nullifier پنهان ساخته شده است.
در کد قرارداد تورنادو کش (Tornado Cash)، این منطق را بهوضوح میتوان در تابع withdraw مشاهده کرد که تصویر آن در پایین قرار گرفته است:
جمعبندی: چه چیزی باید اثبات شود؟
کاربر برای برداشت موفق از تورنادو کش (Tornado Cash) باید سه چیز را اثبات کند:
-
او ورودی هش (preimage) یکی از برگهای درخت مرکل را میداند.
-
مقدار nullifier ارائهشده تاکنون استفاده نشده است. (این بررسی از طریق یک
mappingدر سالیدیتی انجام میشود و بخشی از اثبات دانش صفر نیست.) -
او میتواند هش nullifier را تولید کند و همچنین ورودی هش مربوط به آن را بشناسد.
خروجیهای ممکن در صورت خطا
در صورتی که کاربر در یکی از مراحل بالا اشتباه کند، نتیجه بهشکل زیر خواهد بود:
-
اگر nullifier اشتباه ارائه شود: اثبات دانش صفر برای بررسی nullifier و ورودی هش آن شکست میخورد.
-
اگر عدد محرمانه دوم (secret) اشتباه باشد: اثبات دانش صفر برای برگ درخت مرکل معتبر نخواهد بود، چون ورودی هش صحیح ارائه نشده است.
-
اگر هش nullifier نادرست باشد (برای دور زدن چک ساده در خط 86 قرارداد): اثبات دانش صفر برای nullifier و ورودی هش آن رد خواهد شد.
درخت مرکل افزایشی (Incremental Merkle Tree) و بهینه سازی مصرف گس
شاید متوجه شده باشید که در توضیحات قبلی، یک نکته حیاتی نادیده گرفته شد: چطور ممکن است یک درخت مرکل را روی زنجیره (on-chain) بهروزرسانی کرد بدون اینکه کل گس موجود تمام شود؟
در Tornado Cash، تعداد واریزها ممکن است زیاد باشد، و اگر بخواهیم در هر واریز کل درخت را دوباره محاسبه کنیم، هزینه گس بسیار بالا میرود.
پاسخ این چالش، استفاده از ساختاری به نام درخت مرکل افزایشی (Incremental Merkle Tree) است. این ساختار با استفاده از چند بهینه سازی هوشمندانه، این مشکل را بهخوبی حل میکند.
اما قبل از بررسی این بهینه سازی ها، ابتدا باید محدودیتها و قواعد ساختار آن را درک کنیم.
ساختار درخت مرکل افزایشی: عمق ثابت، رشد مرحلهای
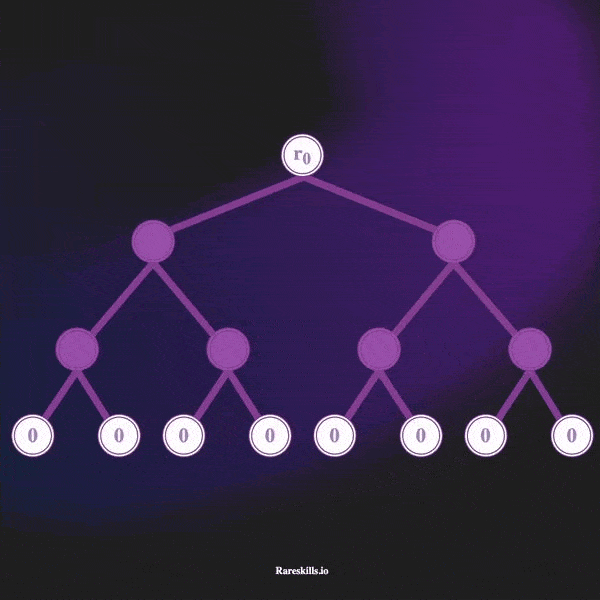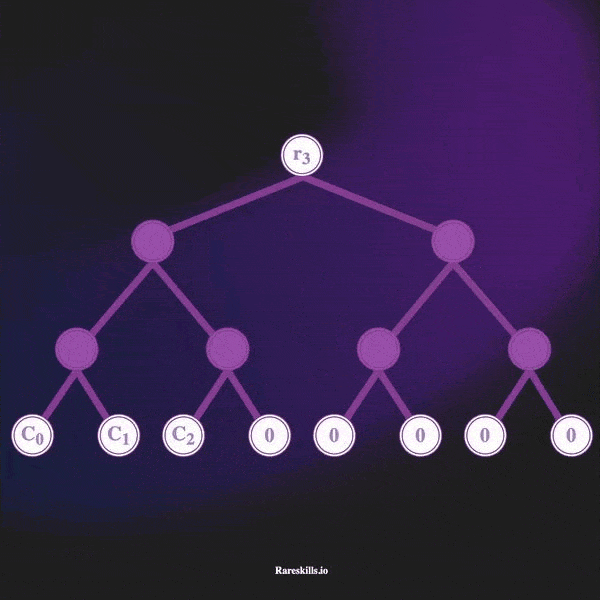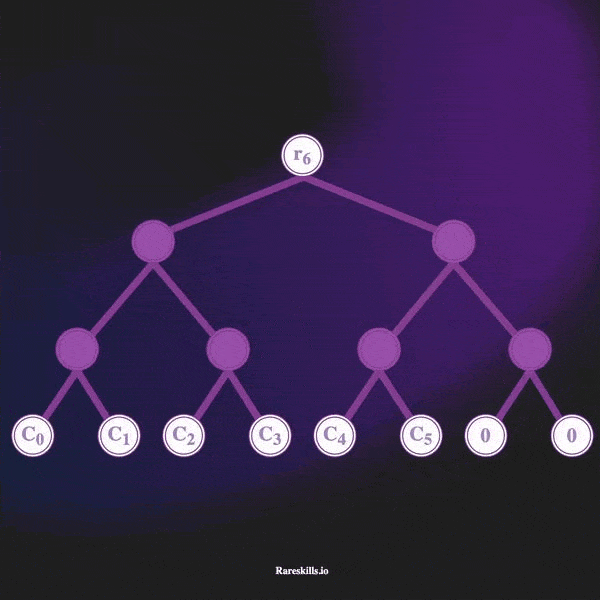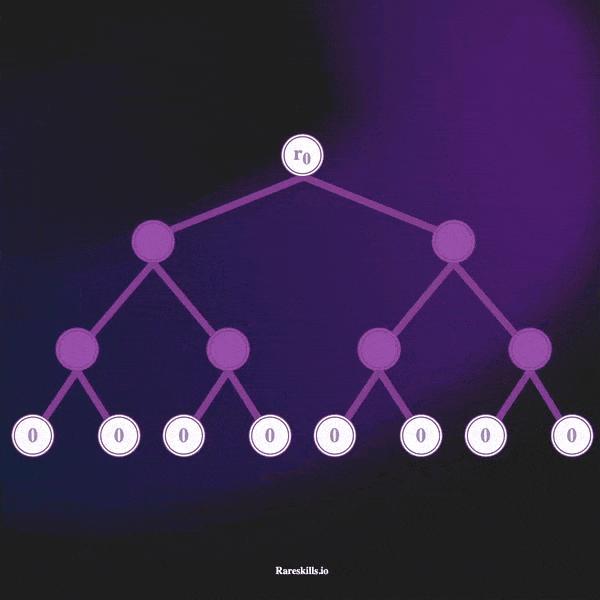
درخت مرکل افزایشی، یک درخت مرکل با عمق ثابت است. در ابتدا، تمام برگهای این درخت با مقدار صفر مقداردهی میشوند. با هر واریز جدید، یکی از این برگهای صفر از سمت چپ به راست با مقدار جدید جایگزین میشود.
این روند بهصورت ترتیبی انجام میشود: برگ شماره ۰ با مقدار جدید جایگزین میشود، سپس برگ ۱، و همینطور تا آخرین برگ موجود.
برای مثال، اگر عمق درخت برابر ۳ باشد، این ساختار میتواند حداکثر ۸ برگ (commitment) در خود نگه دارد. در فضای Tornado Cash، به این برگها اصطلاحاً commitments گفته میشود که معمولاً با یک متغیر خاص در کد مشخص میشوند.
در تصویر زیر، عملکرد این ساختار بهصورت بصری نمایش داده شده است تا روند افزایشی آن بهتر درک شود.
ویژگیهای کلیدی درخت مرکل افزایشی در تورنادو کش (Tornado Cash)
درخت مرکل افزایشی (Incremental Merkle Tree) که در Tornado Cash استفاده میشود، چند ویژگی بسیار مهم دارد که آن را برای اجرای روی بلاکچین مناسب میکند:
-
عمق ثابت برابر با ۳۲ دارد. این یعنی ساختار درخت فقط میتواند حداکثر
2^32 - 1واریز (deposit) را مدیریت کند. این عدد بهصورت دلخواه توسط Tornado Cash انتخاب شده، اما نکته مهم این است که باید ثابت باشد تا ساختار درخت تغییر نکند. -
در ابتدا، همه برگها برابر با هش مقدار صفر هستند. بهطور دقیقتر، مقدار اولیه هر برگ
hash(bytes32(0))است. -
واریزها به ترتیب از چپ به راست وارد میشوند. هر بار که کاربر یک واریز انجام میدهد، اولین برگ خالی از سمت چپ با
commitment hashجدید جایگزین میشود. -
برگهای اضافهشده را نمیتوان حذف کرد. پس از واریز، مقدار هش بهصورت دائمی در درخت باقی میماند و هیچ عملیاتی آن را حذف نمیکند.
-
هر واریز جدید، یک ریشه مرکل (Merkle root) جدید تولید میکند. Tornado Cash این ویژگی را Merkle Tree با سابقه (Merkle Tree with history) مینامد. بنابراین Tornado Cash بهجای ذخیرهسازی یک ریشه واحد، یک آرایه از ریشهها را نگهداری میکند. با هر بار واریز، ساختار درخت تغییر میکند و طبیعتاً ریشه جدیدی ساخته میشود.
چالش: مصرف گس بالا برای درختهای بزرگ
ساختن یک درخت مرکل با 2^32 - 1 برگ روی بلاکچین، در عمل باعث تمام شدن گس میشود. حتی فقط محاسبه سطح اول چنین درختی، بیش از ۴ میلیون تکرار (iteration) نیاز دارد که اجرای آن غیرممکن است.
خوشبختانه، محدودیتهای ذاتی درخت مرکل افزایشی، به قرارداد هوشمند اجازه میدهند با استفاده از دو اصل مهم، از یک میانبر محاسباتی بزرگ استفاده کند:
-
تمام زیرشاخههای سمت راست نود فعلی، زیردرختهایی با ارتفاع مشخص هستند که ریشهی آنها همیشه صفر است.
چون هنوز هیچ واریزی در آنها ثبت نشده، نیازی به محاسبه واقعی ندارند. -
تمام گرههای سمت چپ نود فعلی، قبلاً محاسبه شدهاند و میتوان آنها را در حافظه نگه داشت.
در نتیجه، نیازی نیست این بخشها در هر واریز مجدداً محاسبه شوند.
این دو ویژگی به Tornado Cash امکان میدهند تا بدون ساختن کل درخت از ابتدا، ساختار آن را بهصورت افزایشی و با مصرف گس بسیار پایین حفظ کند.
میانبر هوشمند اول: همه زیردرختهای سمت راست، فقط شامل برگهای صفر هستند
یکی از مهمترین بهینه سازیهایی که در درخت مرکل افزایشی استفاده میشود، مربوط به زیردرختهای سمت راست آخرین واریز ثبتشده است.
تمام این زیردرختها، از برگهایی تشکیل شدهاند که مقدارشان صفر است. این یعنی ریشه چنین درختهایی کاملاً قابل پیشبینی و از قبل قابل محاسبه است.
در ابتدای کار، تمام برگهای درخت مقدار 0 دارند. بنابراین در بسیاری از مراحل، بخش زیادی از محاسبات درخت، شامل ساختن زیردرختهایی است که فقط از صفر تشکیل شدهاند.
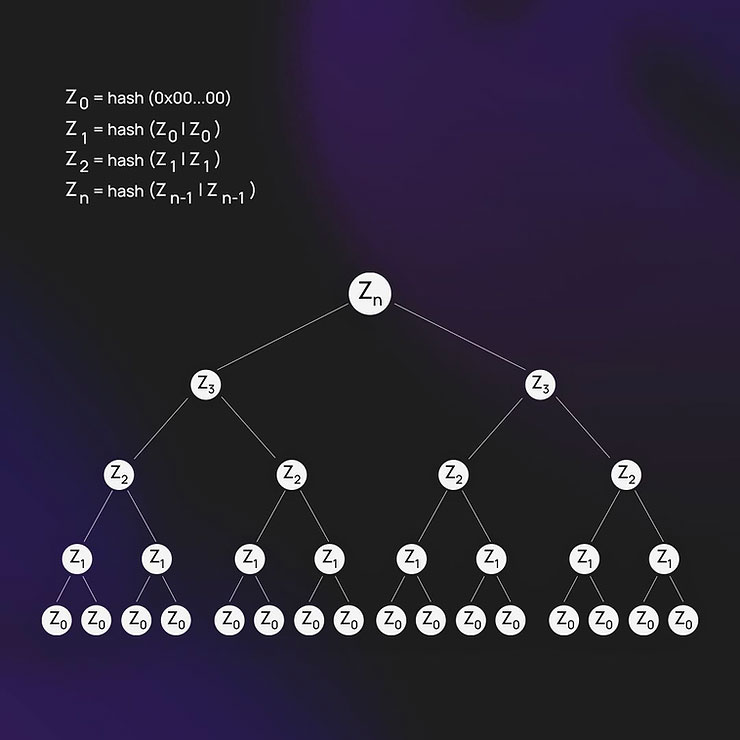
تورنادو کش (Tornado Cash) برای صرفهجویی در مصرف گس، مقادیر زیر را از قبل محاسبه و ذخیره میکند:
-
هش برگ تکی
hash(bytes32(0))(درخت با ارتفاع صفر) -
ریشه زیردرختی با دو برگ صفر
-
ریشه زیردرختی با چهار برگ صفر
-
ریشه زیردرختی با هشت برگ صفر
-
و به همین ترتیب تا سطح ۳۱ از درخت مرکل
از آنجایی که عمق درخت مرکل در Tornado Cash بهصورت ثابت برابر با ۳۲ تعریف شده، امکان محاسبه و ذخیره ریشههای همه زیردرختهای صفر از ارتفاع ۰ تا ۳۱ وجود دارد.
با این پیشمحاسبات، زمانی که قرارداد نیاز دارد یک زیردرخت از برگهای صفر بسازد، فقط کافی است به مقدار از پیشمحاسبهشده برای ارتفاع موردنظر مراجعه کند. دیگر نیازی به انجام محاسبات هش تکراری و پرهزینه نیست.
در ساختار Merkle Tree With History که در Tornado Cash استفاده شده، تمام این مقادیر پیشمحاسبهشده بهصورت یک لیست در قرارداد ذخیره شدهاند:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
/// @dev provides Zero (Empty) elements for a MiMC MerkleTree. Up to 32 levels function zeros(uint256 i) public pure returns (bytes32) { if (i == 0) return bytes32(0x2fe54c60d3acabf3343a35b6eba15db4821b340f76e741e2249685ed4899af6c); else if (i == 1) return bytes32(0x256a6135777eee2fd26f54b8b7037a25439d5235caee224154186d2b8a52e31d); else if (i == 2) return bytes32(0x1151949895e82ab19924de92c40a3d6f7bcb60d92b00504b8199613683f0c200); else if (i == 3) return bytes32(0x20121ee811489ff8d61f09fb89e313f14959a0f28bb428a20dba6b0b068b3bdb); else if (i == 4) return bytes32(0x0a89ca6ffa14cc462cfedb842c30ed221a50a3d6bf022a6a57dc82ab24c157c9); else if (i == 5) return bytes32(0x24ca05c2b5cd42e890d6be94c68d0689f4f21c9cec9c0f13fe41d566dfb54959); else if (i == 6) return bytes32(0x1ccb97c932565a92c60156bdba2d08f3bf1377464e025cee765679e604a7315c); else if (i == 7) return bytes32(0x19156fbd7d1a8bf5cba8909367de1b624534ebab4f0f79e003bccdd1b182bdb4); else if (i == 8) return bytes32(0x261af8c1f0912e465744641409f622d466c3920ac6e5ff37e36604cb11dfff80); else if (i == 9) return bytes32(0x0058459724ff6ca5a1652fcbc3e82b93895cf08e975b19beab3f54c217d1c007); else if (i == 10) return bytes32(0x1f04ef20dee48d39984d8eabe768a70eafa6310ad20849d4573c3c40c2ad1e30); else if (i == 11) return bytes32(0x1bea3dec5dab51567ce7e200a30f7ba6d4276aeaa53e2686f962a46c66d511e5); else if (i == 12) return bytes32(0x0ee0f941e2da4b9e31c3ca97a40d8fa9ce68d97c084177071b3cb46cd3372f0f); else if (i == 13) return bytes32(0x1ca9503e8935884501bbaf20be14eb4c46b89772c97b96e3b2ebf3a36a948bbd); else if (i == 14) return bytes32(0x133a80e30697cd55d8f7d4b0965b7be24057ba5dc3da898ee2187232446cb108); else if (i == 15) return bytes32(0x13e6d8fc88839ed76e182c2a779af5b2c0da9dd18c90427a644f7e148a6253b6); else if (i == 16) return bytes32(0x1eb16b057a477f4bc8f572ea6bee39561098f78f15bfb3699dcbb7bd8db61854); else if (i == 17) return bytes32(0x0da2cb16a1ceaabf1c16b838f7a9e3f2a3a3088d9e0a6debaa748114620696ea); else if (i == 18) return bytes32(0x24a3b3d822420b14b5d8cb6c28a574f01e98ea9e940551d2ebd75cee12649f9d); else if (i == 19) return bytes32(0x198622acbd783d1b0d9064105b1fc8e4d8889de95c4c519b3f635809fe6afc05); else if (i == 20) return bytes32(0x29d7ed391256ccc3ea596c86e933b89ff339d25ea8ddced975ae2fe30b5296d4); else if (i == 21) return bytes32(0x19be59f2f0413ce78c0c3703a3a5451b1d7f39629fa33abd11548a76065b2967); else if (i == 22) return bytes32(0x1ff3f61797e538b70e619310d33f2a063e7eb59104e112e95738da1254dc3453); else if (i == 23) return bytes32(0x10c16ae9959cf8358980d9dd9616e48228737310a10e2b6b731c1a548f036c48); else if (i == 24) return bytes32(0x0ba433a63174a90ac20992e75e3095496812b652685b5e1a2eae0b1bf4e8fcd1); else if (i == 25) return bytes32(0x019ddb9df2bc98d987d0dfeca9d2b643deafab8f7036562e627c3667266a044c); else if (i == 26) return bytes32(0x2d3c88b23175c5a5565db928414c66d1912b11acf974b2e644caaac04739ce99); else if (i == 27) return bytes32(0x2eab55f6ae4e66e32c5189eed5c470840863445760f5ed7e7b69b2a62600f354); else if (i == 28) return bytes32(0x002df37a2642621802383cf952bf4dd1f32e05433beeb1fd41031fb7eace979d); else if (i == 29) return bytes32(0x104aeb41435db66c3e62feccc1d6f5d98d0a0ed75d1374db457cf462e3a1f427); else if (i == 30) return bytes32(0x1f3c6fd858e9a7d4b0d1f38e256a09d81d5a5e3c963987e2d4b814cfab7c6ebb); else if (i == 31) return bytes32(0x2c7a07d20dff79d01fecedc1134284a8d08436606c93693b67e333f671bf69cc); else revert("Index out of bounds"); } |
هنگامی که میخواهیم ریشه درخت مرکل (Merkle root) را محاسبه کنیم، همیشه میدانیم که در کدام سطح z از درخت قرار داریم.
در این حالت، نیازی نیست برای ساخت زیردرختی با برگهای صفر، محاسبات جدیدی انجام دهیم. کافی است به لیست ریشه های از پیشمحاسبهشده مراجعه کنیم و مقدار مربوط به همان سطح را برداریم.
نکته فنی درباره «ریشه های صفر» در تورنادو کش (Tornado Cash)
در واقع، Tornado Cash از مقدار hash(bytes32(0)) بهعنوان مقدار خالی (empty value) در ساختار درخت مرکل استفاده نمیکند. بهجای آن، از hash("tornado") بهعنوان مقدار پایه برای برگ های صفر استفاده شده است.
البته این تفاوت، در منطق یا ساختار الگوریتم تغییری ایجاد نمیکند. چون در نهایت، با یک مقدار ثابت سروکار داریم.
با این حال، برای ساده سازی بحث درباره درخت مرکل افزایشی (Incremental Merkle Tree)، استفاده از واژه «صفر» برای اشاره به این مقدار ثابت راحتتر است تا اینکه بخواهیم در هر مرحله از عبارت «هش رشته tornado» استفاده کنیم.
بنابراین در تمام توضیحات قبلی و بعدی، منظور از «ریشه صفر» یا «برگ صفر» در واقع همان مقدار ثابتی است که Tornado Cash بهعنوان مقدار اولیه استفاده میکند، حتی اگر از نظر فنی hash("tornado") باشد.
میانبر هوشمند دوم: ذخیره سازی (Cache) ریشه های زیردرخت های سمت چپ بهجای محاسبه مجدد
دومین بهینه سازی مهم در ساختار درخت مرکل افزایشی به زیردرخت های سمت چپ آخرین واریز مربوط میشود.
فرض کنیم کاربر دوم در حال انجام واریز است. ما قبلاً هش واریز اول را محاسبه کردهایم. بهجای اینکه دوباره این هش را برای ساخت ریشه مرکل محاسبه کنیم، قرارداد هوشمند Tornado Cash آن را در یک متغیر ذخیره میکند. این متغیر یک mapping است که با نام filledSubtrees شناخته میشود.
filledSubtree یعنی چه؟
درختهای مرکل از چند زیردرخت تشکیل شدهاند. هر زمانی که یک زیردرخت کاملاً پر شده باشد (یعنی همه برگهای آن مقدار غیر صفر داشته باشند)، آن زیردرخت بهعنوان یک filledSubtree شناخته میشود.
Tornado Cash برای هر سطح از درخت، آخرین filledSubtree محاسبهشده را ذخیره میکند و در هنگام واریزهای جدید، بهجای محاسبه مجدد، مستقیماً از آن استفاده میکند.
در انیمیشن آموزشی Tornado Cash، این زیردرختها با نماد fs مشخص شدهاند:
نکته اینجاست که هر زمان به یک هش میانی (intermediate hash) در سمت چپ نیاز داشته باشید، آن مقدار قبلاً برایتان محاسبه شده است.
این ویژگی مفید، نتیجه مستقیم این محدودیت است که: برگها (commitments) در درخت مرکل افزایشی قابل تغییر یا حذف نیستند.
وقتی یک زیردرخت با مقادیر واقعی (و نه صفر) پر میشود، دیگر هرگز نیاز به محاسبه مجدد آن نداریم.
حالا بیایید این موضوع را کمی تعمیم دهیم. بهجای اینکه گره سمت چپ را فقط بهعنوان «اولین واریز» ببینیم، تصور کنید خود آن گره، ریشه یک زیردرخت کامل است.
در شدیدترین حالت ممکن، زمانی را در نظر بگیرید که داریم آخرین برگ درخت را وارد میکنیم. ساختار سمت چپ ما به شکل زیر خواهد بود:
-
دقیقاً سمت چپ ما، یک درخت کوچک با عمق صفر است که فقط شامل برگ ماقبل آخر میشود
-
سمت چپ آن، زیردرختی با عمق ۱ قرار دارد (۲ برگ)
-
سپس زیردرختی با عمق ۲ قرار میگیرد (۴ برگ)
-
بعدی، زیردرختی با عمق ۳ خواهد بود (۸ برگ)
-
و این روند همینطور ادامه پیدا میکند…
در شدیدترین حالت، بیشتر از ۳۲ زیردرخت نخواهیم داشت، چون عمق درخت مرکل در تورنادو کش (Tornado Cash) بهصورت ثابت روی عدد ۳۲ تنظیم شده است.
ترکیب میانبرها
تمام گرههایی که در سمت چپ ما قرار دارند، یک زیردرخت پر (filled subtree) هستند، حتی اگر فقط یک برگ باشند. و هر چیزی که در سمت راست ما قرار دارد، همیشه یا برگ صفر است، یا یک زیردرختی که تمام برگهای آن صفر هستند.
از آنجایی که ریشه زیردرختهای سمت چپ را کش میکنیم (cached)، و ریشه زیردرختهای صفر سمت راست را از قبل محاسبه کردهایم، میتوانیم هر ترکیب میانی از هشها (intermediate hash concatenation) را در هر سطحی از درخت، بهصورت کارآمد محاسبه کنیم.
به همین دلیل، میتوانیم درخت مرکل با عمق ۳۲ را روی بلاکچین، فقط با ۳۲ تکرار (iteration) بسازیم.
درست است، این کار کاملاً ارزان نیست، اما کاملاً قابل اجرا روی زنجیره (on-chain) است. و قطعاً بسیار بهتر از این است که مجبور باشیم ۴ میلیون محاسبه انجام دهیم!
هشِ چپ یا هشِ راست؟
وقتی داریم مسیر خود را تا ریشه درخت مرکل پیش میرویم، یعنی مرحلهبهمرحله هشها را به سمت بالا ترکیب میکنیم، یک سؤال مهم پیش میآید:
از کجا بفهمیم ترتیب چسباندن (concatenate) هشهای زیردرختها به چه صورت باید باشد؟
مثلاً فرض کنیم یک commitment hash جدید داریم و میخواهیم آن را بهعنوان یک برگ جدید به درخت اضافه کنیم. در گره بالایی، آیا باید هش را به این صورت بچسبانیم؟
|
1 |
new_commitment | other_value |
|
1 |
other_value | new_commitment |
در اینجا یک قانون ساده اما بسیار مهم به کمک ما میآید:
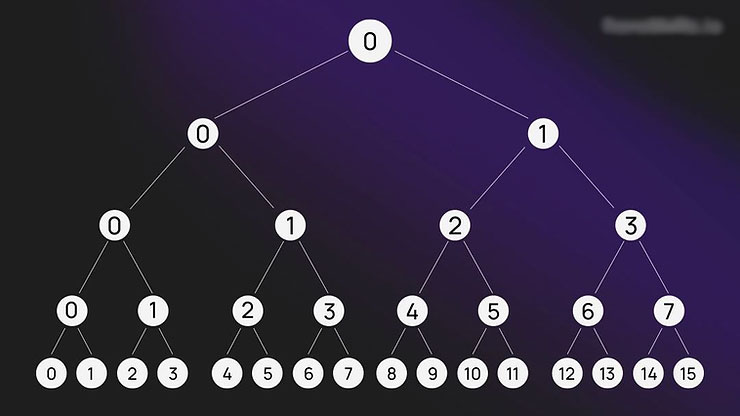
هر گره با ایندکس زوج (even index)، گره سمت چپ است.
هر گره با ایندکس فرد (odd index)، گره سمت راست است.
این قانون برای همه سطوح درخت مرکل صدق میکند، چه گرههای برگ (leaf nodes) و چه گرههای میانی یا بالاتر.
یعنی با دانستن ایندکس گره، همیشه میدانیم موقعیت آن در درخت چیست و در نتیجه میفهمیم ترتیب ترکیب هش ها چگونه باید باشد. در دیاگرام زیر، این الگوی مرتبسازی و چیدمان گرهها بهوضوح نمایش داده شده است:
برای اینکه بهتر الگو را درک کنیم، بیایید یک مثال ساده را بررسی کنیم:
اگر اولین برگ (برگ با ایندکس صفر) در حال اضافهشدن باشد، در مسیر رسیدن به ریشه، فقط عملیات هشِ راست (hash right) انجام میدهیم.
چرا؟ چون 0 ÷ 2 = 0 و طبق قانونی که قبلاً گفتیم، صفر یک عدد زوج است. وقتی ایندکس زوج باشد، یعنی ما در سمت چپ قرار داریم، و بنابراین باید هش سمت راست را با هش فعلی ترکیب کنیم.
حالا برویم به سمت دیگر طیف:
اگر آخرین برگ درخت را وارد کنیم، در مسیر رسیدن به ریشه، در هر مرحله باید هشِ چپ (hash left) انجام دهیم. چرا؟ چون تمام گرههایی که در مسیر بالا قرار میگیرند، ایندکس فرد دارند.
تعمیم این الگو به تمام گرهها
این الگو فقط برای حالت های مرزی نیست؛ برای هر گرهای در وسط درخت هم، کافی است مراحل زیر را انجام دهید:
-
ایندکس برگ موردنظر را در نظر بگیرید.
-
آن را تقسیم بر ۲ کنید و به عدد صحیح پایینتر گرد کنید.
-
بررسی کنید عدد حاصل زوج است یا فرد.
-
اگر زوج باشد: شما در سمت چپ هستید → باید هش سمت راست را اضافه کنید
-
اگر فرد باشد: شما در سمت راست هستید → باید هش سمت چپ را اضافه کنید
-
با ادامهدادن این روند تا ریشه درخت، میتوانید در هر سطح دقیقاً تشخیص دهید باید هش را از کدام سمت ترکیب کنید.
در انیمیشن زیر، دقیقاً این روند نمایش داده شده: وقتی در گره با ایندکس فرد قرار دارید، هش سمت چپ انجام میشود؛ وقتی در گره با ایندکس زوج هستید، هش سمت راست انجام میشود.
بنابراین، در هر سطح درخت، میدانیم هش فعلی باید در کدام سمت نسبت به گره خواهر (sibling) قرار بگیرد
بههمین دلیل، برای ساختن مسیر درست از برگ تا ریشه، فقط به دو اطلاعات نیاز داریم:
-
ایندکس گرهای که داریم آن را وارد میکنیم
-
زوج یا فرد بودن ایندکس فعلی
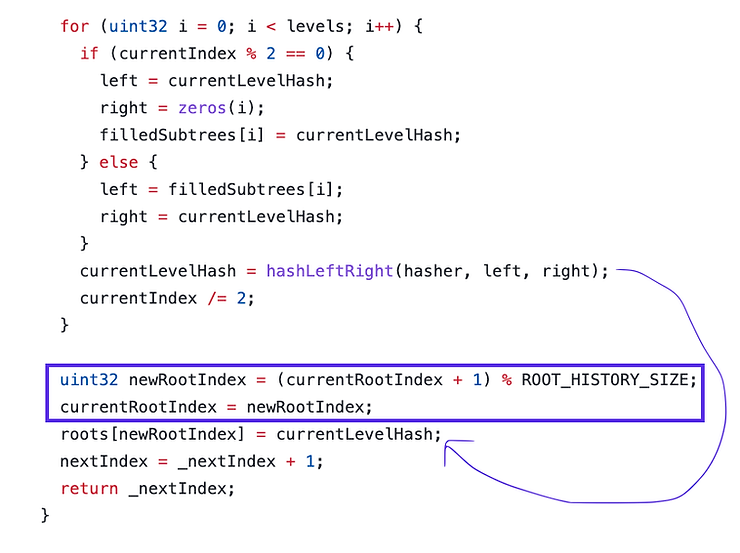
در تصویر زیر (از کد منبع Tornado Cash)، دقیقاً همین منطق پیادهسازی شده است. در اینجا، یک حلقه for روی تمام سطوح درخت تکرار میشود تا ریشه جدید Merkle Tree بر اساس برگ تازهوارد محاسبه شود.
خلاصه فرآیند بهروزرسانی Merkle Root روی بلاکچین
برای بهروزرسانی ریشه درخت مرکل روی زنجیره (on-chain)، مراحل زیر را دنبال میکنیم:
-
یک برگ جدید به درخت اضافه میکنیم و آن را به متغیر
currentIndexاختصاص میدهیم. -
به سطح بالاتر درخت میرویم و مقدار
currentIndexرا بر ۲ تقسیم میکنیم. -
حالا بسته به مقدار
currentIndex، یکی از این دو مسیر را طی میکنیم:-
اگر
currentIndexفرد باشد: باید هش از سمت چپ انجام دهیم و از مقدار ذخیره شده درfilledSubtreesاستفاده کنیم. -
اگر
currentIndexزوج باشد: باید هش از سمت راست انجام دهیم و از ریشههای از پیشمحاسبهشده زیردرختهای صفر (precomputed zero-tree) استفاده کنیم.
-
واقعاً جالب است که چنین الگوریتمی، با اینهمه جزئیات و پیچیدگی منطقی، در قالب یک کد نسبتاً کوچک در سالیدیتی قابل پیاده سازی است.
Tornado Cash آخرین ۳۰ ریشه (Root) را ذخیره میکند، چون با هر واریز، ریشه تغییر میکند
هر بار که یک برگ جدید وارد درخت مرکل میشود، ریشهی درخت (Merkle Root) حتماً تغییر میکند. این تغییر مداوم ممکن است برای کاربر برداشتکننده مشکلساز شود. فرض کنید:
-
کاربر برداشتکننده، برای آخرین ریشه درخت، یک Merkle proof تولید کرده است (چون برگها عمومی هستند، این کار امکانپذیر است).
-
اما قبل از اینکه تراکنش برداشت خود را ارسال کند، یک واریز دیگر ثبت میشود.
-
در این صورت، ریشه درخت عوض میشود و Merkle proof قبلی دیگر معتبر نخواهد بود.
الگوریتم تأیید zk-proof، بررسی میکند که Merkle proof واقعاً با ریشهای که ارائه شده مطابقت داشته باشد. بنابراین اگر ریشه تغییر کرده باشد، اثبات رد خواهد شد.
راهحل تورنادو کش (Tornado Cash): ذخیره چند ریشه اخیر
برای اینکه کاربر برداشتکننده فرصت کافی برای ارسال برداشت داشته باشد، قرارداد هوشمند Tornado Cash اجازه میدهد که کاربر، تا ۳۰ ریشه آخر را بهعنوان مرجع در Merkle proof خود استفاده کند.
متغیر roots در قرارداد، یک mapping است که از uint256 به bytes32 نگاشت میکند. وقتی محاسبات Merkle proof به پایان میرسد و ریشه جدید ساخته میشود، آن مقدار در این mapping ذخیره میشود.
متغیر currentRootIndex نیز در هر مرحله افزایش پیدا میکند تا به حداکثر مقدار یعنی ROOT_HISTORY_SIZE (عدد ۳۰) برسد. اگر این مقدار از ۳۰ عبور کند، مقدار جدید، روی ایندکس صفر بازنویسی میشود. بنابراین، این ساختار مانند یک صف با اندازه ثابت (Fixed-Size Queue) عمل میکند.
در بخش زیر، بخشی از تابع _insert از کد درخت مرکل تورنادو کش (Tornado Cash) نمایش داده شده است. در این تابع، پس از محاسبه ریشه جدید، ریشه مطابق همین منطق در متغیر roots ذخیره میشود.
متغیرهای ذخیره سازی برای درخت مرکل افزایشی با نگهداری ریشههای قبلی (Incremental Merkle Tree with History)
برای اینکه ساختار درخت مرکل افزایشی با امکان ذخیرهسازی با نگهداری ریشههای قبلی (Merkle Tree with history) بهدرستی کار کند، مجموعهای از متغیرهای ذخیره سازی (storage variables) در قرارداد تعریف شدهاند:
|
1 2 3 4 5 |
mapping(uint256 => bytes32) public filledSubtrees; mapping(uint256 => bytes32) public roots; uint32 public constant ROOT_HISTORY_SIZE = 30; uint32 public currentRootIndex = 0; uint32 public nextIndex = 0; |
در ادامه توضیح هرکدام از این متغیرها آورده شده است:
-
filledSubtrees: این متغیر، زیردرختهایی را ذخیره میکند که قبلاً بهطور کامل با برگهای غیرصفر پر شدهاند. این همان کش (cache) هشهایی است که دیگر نیازی به محاسبه مجدد آنها نیست.
-
roots: در این
mapping، ۳۰ ریشه آخر درخت مرکل ذخیره میشوند. این متغیر برای اطمینان از اعتبار Merkle proofها در صورت وقوع واریزهای متوالی طراحی شده است. -
currentRootIndex: این مقدار، ایندکس فعلی در آرایه
rootsرا مشخص میکند. این عدد همیشه بین ۰ تا ۲۹ قرار دارد و به صورت چرخشی (circular) بروزرسانی میشود. -
nextIndex: این متغیر مشخص میکند که اگر کاربر تابع
depositرا فراخوانی کند، برگ بعدی که قرار است در درخت پر شود، چه ایندکسی خواهد داشت.
عملکرد تابع عمومی deposit() و بهروزرسانی درخت مرکل با نگهداری ریشههای قبلی
زمانی که کاربر تابع deposit را در Tornado Cash فراخوانی میکند، ابتدا تابع داخلی _insert() اجرا میشود تا مقدار جدید وارد درخت مرکل با نگهداری ریشههای قبلی شود. سپس تابع _processDeposit() اجرا میشود تا صحت مبلغ واریزی بررسی گردد. کد مربوط به تابع deposit() بهصورت زیر است:
|
1 2 3 4 5 6 7 8 9 |
function deposit(bytes32 _commitment) external payable nonReentrant { require(!commitments[_commitment], "The commitment has been submitted"); uint32 insertedIndex = _insert(_commitment); commitments[_commitment] = true; _processDeposit(); emit Deposit(_commitment, insertedIndex, block.timestamp); } |
تابع _processDeposit() فقط یک کار ساده انجام میدهد: بررسی میکند که مبلغ ارسالی با مقدار استاندارد مورد نظر (denomination) تطابق دارد. این مقدار میتواند مثلاً ۰.۱، ۱ یا ۱۰ اتر باشد، بسته به اینکه با کدام نسخه از Tornado Cash تعامل دارید. کد این تابع بهصورت زیر است:
|
1 2 3 |
function _processDeposit() internal override { require(msg.value == denomination, "Please send `mixDenomination` ETH along with transaction"); } |
هش MiMC فوق بهینه شده (Hyperoptimized MiMC Hash)
برای محاسبه ریشه درخت مرکل روی زنجیره (on-chain)، طبیعتاً باید از یک الگوریتم هش استفاده کنیم. اما نکته جالب این است که تورنادو کش (Tornado Cash) از هش رایج keccak256 استفاده نمیکند؛ بلکه بهجای آن، از الگوریتمی بهنام MiMC استفاده میکند.
دلیل این انتخاب کمی خارج از محدوده این مقاله است، اما بهصورت خلاصه:
برخی الگوریتمهای هش برای تولید اثبات دانش صفر (Zero Knowledge Proof) بسیار ارزانتر و مناسبتر هستند. MiMC بهطور خاص برای «سازگاری با دانش صفر» (zk-friendly) طراحی شده، در حالی که keccak256 چنین نیست.
وقتی میگوییم یک الگوریتم هش “zk-friendly” است، یعنی:
الگوریتم بهگونهای طراحی شده که ساختار آن با نحوه نمایش محاسبات در اثباتهای دانش صفر تطبیق طبیعی دارد. در نتیجه، زمان تولید zk-proof بسیار کاهش مییابد.
اما این انتخاب یک چالش جدید ایجاد میکند…
چون الگوریتم MiMC باید برای محاسبه ریشه جدید Merkle Tree روی زنجیره اجرا شود، و اتریوم هیچ قرارداد از پیشکامپایلشده (precompiled contract) برای هشهای zk-friendly ندارد، تیم تورنادو کش (Tornado Cash) مجبور شد این الگوریتم را بهصورت دستی با bytecode خام (raw bytecode) پیادهسازی کند.
اگر به صفحه قرارداد تورنادو کش (Tornado Cash) در Etherscan نگاه کنید، احتمالاً با این هشدار روبهرو میشوید:
Etherscan نمیتواند bytecode خام را به Solidity تبدیل کند، چون MiMC با زبان Solidity نوشته نشده است.
پیادهسازی MiMC بهصورت قرارداد مستقل
تیم Tornado Cash الگوریتم MiMC را بهعنوان یک قرارداد هوشمند مستقل پیادهسازی کرده است. برای استفاده از این هش، کد درخت مرکل Tornado Cash یک فراخوانی بینقراردادی (cross-contract call) به آن قرارداد انجام میدهد.
همانطور که در کد زیر میبینید، این فراخوانیها static هستند، چون تابع بهصورت pure تعریف شده است. به همین دلیل است که در Etherscan برای این قرارداد هیچ سابقه تراکنشی نمایش داده نمیشود.
|
1 2 3 |
interface IHasher { function MiMCSponge(uint256 in_xL, uint256 in_xR) external pure returns (uint256 xL, uint256 xR); } |
ما میدانیم که استفاده از این تابع از طریق interface انجام شده، چون کد مربوط به Tornado Cash در GitHub (ارجاع دادهشده در بالا) این را نشان میدهد.
در یکی از issueهای GitHub در مخزن Circom library توضیح داده شده که چرا کد MiMC با استفاده از Solidity حتی با بلاکهای اسمبلی، قابل پیادهسازی نیست. دلیلش ساده است: در EVM امکان دستکاری مستقیم استک (stack) در سطح پایین وجود ندارد.
پیاده سازی تابع هش اختصاصی با استفاده از Bytecode خام
مخزن circomlib-js شامل ابزارهای جاوااسکریپتی برای تولید نسخه Bytecode خام از الگوریتمهای هش سفارشی است. با استفاده از این ابزارها، میتوان الگوریتمهایی مانند MiMC یا Poseidon Hash را بهصورت مستقیم و بدون وابستگی به زبان سالیدیتی، برای اجرا روی زنجیره آماده کرد.
برداشت از Tornado Cash
برای شروع فرآیند برداشت، کاربر باید ابتدا درخت مرکل را بهصورت محلی (لوکال) بازسازی کند. برای این کار، از اسکریپت updateTree استفاده میشود که تمام رویدادهای مربوطه را از قرارداد هوشمند دانلود کرده و درخت مرکل را دوباره تولید میکند.
پس از بازسازی درخت، کاربر باید یک اثبات دانش صفر (Zero Knowledge Proof) تولید کند که شامل:
-
Merkle proof
-
و ورودیهای هش (preimages) برای برگ (leaf commitment) و nullifier
همانطور که قبلاً گفته شد، Tornado Cash همیشه ۳۰ ریشه آخر درخت مرکل را نگه میدارد. بنابراین، کاربر معمولاً فرصت کافی دارد تا اثبات خود را ارسال کند. اما اگر کاربر خیلی دیر اقدام کند، باید Merkle proof را دوباره با ریشهای جدید بازتولید کند.
بررسیهایی که قرارداد Tornado Cash هنگام برداشت انجام میدهد:
-
بررسی میشود که
nullifierHashارسالی قبلاً استفاده نشده باشد. -
بررسی میشود که ریشه Merkle (
_root) جزو ۳۰ ریشه آخر ذخیرهشده باشد. -
اثبات دانش صفر باید معتبر باشد. این شامل بررسی موارد زیر است:
a. ورودی هش پنهانشده (preimage) باید همان برگی را تولید کند که در Merkle proof استفاده شده است
b. کاربر باید واقعاً ورودی
nullifierHashرا بشناسدc. Merkle proof باید نشان دهد که آن برگ به ریشه Merkle مشخصشده منتهی میشود
d. این ریشه Merkle باید یکی از ۳۰ ریشه ذخیرهشده در قرارداد باشد (این بخش مستقیماً در کد سالیدیتی بررسی میشود)
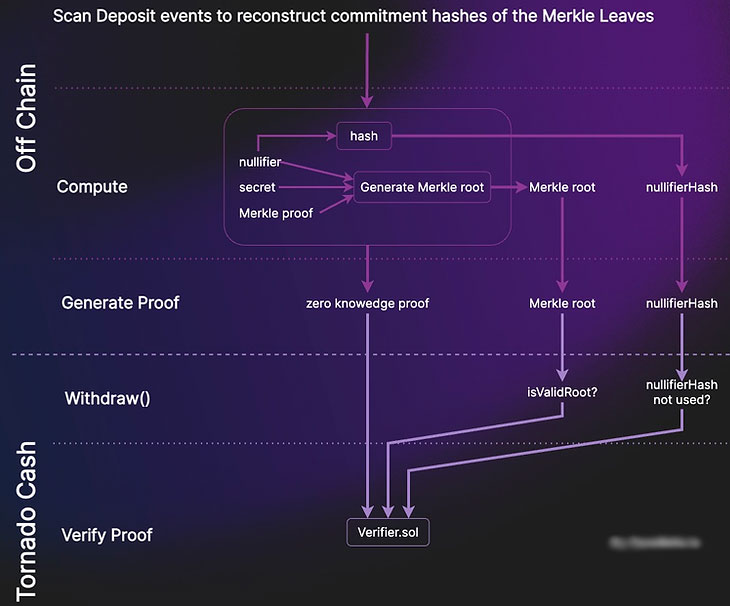
در اینجا، با یک دیاگرام از فرآیند برداشت نمایش داده شده است که مراحل بالا را بهصورت تصویری خلاصه میکند:
حالا نگاهی به کد تابع withdraw بیندازیم. درک این تابع پس از توضیحات بالا نسبتاً ساده است:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
function withdraw(bytes calldata _proof, bytes32 _root, bytes32 _nullifierHash, address payable _recipient, address payable _relayer, uint256 _fee, uint256 _refund ) external payable nonReentrant { require(_fee <= denomination, "Fee exceeds transfer value"); require(!nullifierHashes[_nullifierHash], "The note has been already spent"); require(isKnownRoot(_root), "Cannot find your merkle root"); // Make sure to use a recent onerequire( verifier.verifyProof( _proof, [uint256(_root), uint256(_nullifierHash), uint256(_recipient), uint256(_relayer), _fee, _refund] ), "Invalid withdraw proof" ); nullifierHashes[_nullifierHash] = true; _processWithdraw(_recipient, _relayer, _fee, _refund); emit Withdrawal(_recipient, _nullifierHash, _relayer, _fee); } |
متغیرهای _relayer، _fee و _refund مربوط به پرداخت کارمزد به relayer اختیاری هستند، کاربرانی که تراکنش را بهجای شما در بلاکچین منتشر میکنند. در بخش بعدی، دقیقاً توضیح میدهیم که این ساختار چگونه کار میکند و چه مزایایی دارد.
تابع isKnownRoot(root) چه میکند؟
این تابع بررسی میکند که ریشه Merkle ارسالشده (در هنگام برداشت وجه) واقعاً یکی از ۳۰ ریشه آخر درخت مرکل باشد که در قرارداد ذخیره شدهاند.
الگوریتم آن بسیار ساده است و از یک حلقه do-while استفاده میکند. منطق آن به این صورت است:
-
از شاخص فعلی ریشه (currentRootIndex) شروع میکند؛ یعنی آخرین ریشهای که با جدیدترین واریز بهروز شده است.
-
سپس حلقه بهصورت برعکس (backwards) تا حداکثر ۳۰ بار چک میکند که آیا
rootارسالی در میان ۳۰ ریشه اخیر وجود دارد یا نه. -
اگر پیدا کند، مقدار
trueبرمیگرداند. در غیر این صورت، پس از چککردن همه ۳۰ مورد، مقدارfalse.
چون فقط ۳۰ ریشه اخیر بررسی میشود، این حلقه محدود، امن و بهینه از نظر گس (gas) است. ما نگرانیای بابت اجرای حلقهای غیرمحدود یا پرهزینه نداریم.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
/** @dev Whether the root is present in the root history */function isKnownRoot(bytes32 _root) public view returns (bool) { if (_root == 0) { return false; } uint32 _currentRootIndex = currentRootIndex; uint32 i = _currentRootIndex; do { if (_root == roots[i]) { return true; } if (i == 0) { i = ROOT_HISTORY_SIZE; // 30 } i--; } while (i != _currentRootIndex); return false; } |
کد Circom برای تعریف محاسبات اثبات دانش صفر (Zero Knowledge)
این بخش کدهای Circom را توضیح میدهد که برای تولید مدارهایی استفاده میشوند که اعتبار اثبات دانش صفر (ZK Proof) را بررسی میکنند. اگر با Circom آشنا نیستید، در اینجا سعی میکنیم کد Circom را در یک سطح کلی و قابل فهم توضیح دهیم.
کد Circom مستقیماً روی بلاکچین اجرا نمیشود. بلکه ابتدا به کدی در سالیدیتی تبدیل میشود که ظاهر ترسناکی دارد، مثلاً چیزی که در فایل Verifier.sol از تورنادو کش (Tornado Cash) میبینید. دلیل این ظاهر پیچیده این است که آن کد واقعاً دارد ریاضیات مربوط به اعتبارسنجی اثبات ZK را اجرا میکند.
خوشبختانه، خود Circom بسیار خواناتر و قابلفهمتر از نسخه تبدیلشده به Solidity است.
در اینجا ما سه کامپوننت (Component) داریم:
HashLeftRight که وظیفه ترکیب (concatenate) هشها را دارد، DualMux که فقط یک ابزار کمکی برای MerkleTreeChecker است و MerkleTreeChecker.
کامپوننت MerkleTreeChecker سه ورودی میگیرد: یک leaf (برگ درخت مرکل)، یک root (ریشه)، و یک proof (اثبات).
این proof خودش دو بخش دارد:
-
pathElements: شامل ریشه زیردرخت خواهر (sister subtree) در آن سطح از Merkle Tree است.
-
pathIndices: شامل یک اندیس (شاخص) است که به مدار کمک میکند بفهمد در آن سطح، ترتیب چسباندن هشها باید چطور باشد (مثلاً آیا هش فعلی باید در سمت چپ قرار بگیرد یا راست).
خط نهایی این ماژول، یعنی:
|
1 |
root === hashers[levels - 1].hash |
حالا برگردیم به nullifierHash:
این مقدار حاصل هش کردن مقدار nullifier است.
و commitment مقدار حاصل هش کردن ترکیب nullifier و secret میباشد.
در کد Circom، این محاسبه به صورت زیر نمایش داده شده است. هرچند ممکن است در نگاه اول کمی پیچیده به نظر برسد، اما کاملاً روشن است که:
-
ورودیها عبارتند از:
nullifierوsecret -
و خروجیها عبارتند از:
commitmentوnullifierHash
هسته اصلی الگوریتم دانش صفر
اکنون میتوانیم به هسته اصلی الگوریتم دانش صفر (zero knowledge) برسیم.
یک سیگنال خصوصی (private signal) به این معناست که این مقدار بهصورت پنهان در اثبات (proof) قرار دارد، همانطور که قبلاً در ساختار نامگذاری توضیح داده شد.
در کد بالا، ابتدا بررسی میشود که محاسبه nullifierHash به شکل صحیح انجام شده باشد. سپس، تصویر اولیه (preimage) از commitment و مدرک مرکل (Merkle proof) به مدار بررسیکننده Merkle Tree (که قبلاً ساختیم) داده میشود.
اگر همه بررسیها با موفقیت انجام شوند:
verifier مقدار true برمیگرداند، یعنی اثبات معتبر است و در نتیجه، آدرس ناشناس کاربر میتواند مبلغ خود را برداشت کند، بدون اینکه هویت یا دادههای حساسش فاش شود.
جلوگیری از فرانت رانینگ (Frontrunning) هنگام برداشت (withdrawal)
احتمالاً پژوهشگران امنیتی متوجه شدهاند که کد سالیدیتی در بخش برداشت، هیچ دفاع مستقیمی در برابر حملات فرانترانینگ ندارد.
یعنی چی؟ فرض کنید یک کاربر یک اثبات دانش صفر معتبر (valid zk-proof) رو به mempool ارسال میکنه. چه چیزی جلوی یک مهاجم را میگیرد که این اثبات را کپی کند و فقط آدرس برداشت رو به آدرس خودش تغییر بدهد؟!
این موضوعی است که برای ساده سازی از آن عبور کردیم، اما در حقیقت فایل Withdraw.circom شامل سیگنالهای ساختگی (dummy signals) است که آدرس گیرنده (و سایر پارامترهای مورد نیاز برای ریلیرها) را به توان دو میرسانند. این یعنی اثبات دانش صفر (zk-proof) باید نشان دهد که کاربر آدرس گیرنده را به توان دو رسانده و حاصل بهدرستی با مقدار مورد انتظار (مربع آدرس خودش) تطابق دارد. به خاطر داشته باشید که آدرسها فقط اعدادی ۲۰ بایتی هستند.
محاسبه مربع آدرس و همچنین هش nullifier و secret همه در یک فرآیند محاسباتی انجام میشوند، بنابراین اگر هر بخشی از این محاسبه اشتباه باشد، کل اثبات نامعتبر خواهد شد.
ریلیر (Relayer) و کارمزد (Fee) چیست؟
یک ریلیر (Relayer) در واقع یک ربات آفلاین است که به جای کاربران دیگر هزینه گس (Gas) را پرداخت میکند و در ازای آن، نوعی پرداخت دریافت میکند. در سیستم تورنادو کش (Tornado Cash)، اغلب افرادی که قصد برداشت دارند میخواهند از آدرسهای کاملاً جدید استفاده کنند تا حریم خصوصیشان بیشتر حفظ شود. اما مشکل اینجاست که این آدرسهای تازهساختهشده هیچ اتریومی ندارند که بتواند هزینه گس برای برداشت را پرداخت کند.
برای حل این مشکل، کاربر میتواند از یک ریلیر درخواست کند که تراکنش برداشت را بهجای او انجام دهد. در مقابل، ریلیر بخشی از مبلغ برداشتشده را بهعنوان کارمزد دریافت میکند.
آدرس برداشت ریلیر هم باید از همان مکانیزم محافظتی در برابر فرانترانینگ که پیشتر توضیح داده شد استفاده کند. این موضوع در اسکرینشات کد بالا قابل مشاهده است.
خلاصهای از روند deposit() و withdraw()
زمانی که deposit() فراخوانی میشود:
-
کاربر هشِ ترکیبشده
(nullifier + secret)را همراه با مبلغ ارز دیجیتالی که قصد واریز آن را دارد ارسال میکند. -
Tornado Cash بررسی میکند که مبلغ واریزشده مطابق یکی از مقادیر ثابت تعیینشده باشد (مثلاً فقط ۰.۱، ۱ یا ۱۰ اتریوم).
-
Tornado Cash این commitment را بهعنوان برگ بعدی در درخت Merkle ثبت میکند. برگها هرگز حذف نمیشوند.
زمانی که withdraw() فراخوانی میشود:
-
کاربر باید درخت Merkle را بهصورت محلی (لوکال) بازسازی کند، بر اساس ایونتهایی که Tornado Cash قبلاً منتشر کرده.
-
کاربر باید سه مورد ارائه کند:
-
هشِ nullifier (به صورت عمومی)
-
ریشه Merkle که قرار است اعتبارسنجی شود
-
یک اثبات zero-knowledge (zk proof) مبنی بر اینکه او واقعاً nullifier، secret و مسیر Merkle را میداند
-
-
Tornado Cash بررسی میکند که این nullifier قبلاً استفاده نشده باشد.
-
Tornado Cash بررسی میکند که ریشهی ارائهشده یکی از ۳۰ ریشهی آخر ذخیرهشده باشد.
-
Tornado Cash بررسی میکند که اثبات zk معتبر باشد.
نکته امنیتی: هیچ چیزی جلوی یک کاربر را نمیگیرد که یک commitment کاملاً نامعتبر (بدون preimage شناختهشده) ثبت کند. در این صورت، ارز دیجیتال ارسالی او برای همیشه در قرارداد گیر خواهد کرد و قابل برداشت نیست.
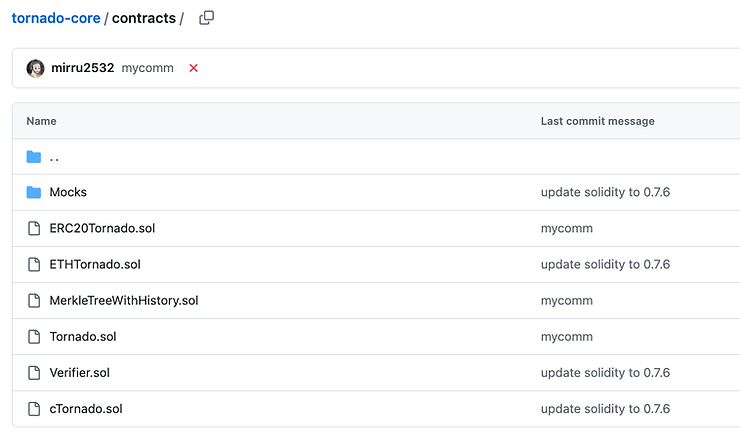
مرور سریع معماری قراردادهای هوشمند در تورنادو کش (Tornado Cash)
در ادامه، اجزای اصلی تشکیلدهنده پروتکل Tornado Cash را معرفی میکنیم:
Tornado.sol یک قرارداد انتزاعی (abstract) است که هسته عملکرد پروتکل را تعریف میکند. این قرارداد بسته به نوع دارایی، به دو شکل پیادهسازی میشود:
-
ETHTornado.sol: مخصوص مخلوطکردن مقدار مشخصی از اتریوم -
ERC20Tornado.sol: مخصوص مخلوطکردن توکنهای ERC20
برای هر توکن ERC20 و هر مقدار مشخص اتریوم (مثلاً ۰.۱، ۱ یا ۱۰ ETH)، یک نمونهی جداگانه از Tornado Cash ایجاد میشود.
قرارداد MerkleTreeWithHistory.sol شامل توابع مهمی است که قبلاً با جزئیات بررسی کردیم:
-
_insert(): افزودن برگ جدید (commitment) به درخت Merkle -
isKnownRoot(): بررسی اینکه آیا ریشهای که کاربر ارائه داده، در بین ۳۰ ریشه اخیر قرار دارد یا نه
Verifier.sol خروجی کامپایلشده کدهای Circom به زبان Solidity است. این قرارداد ریاضی مربوط به اعتبارسنجی اثبات zero-knowledge را انجام میدهد. هرچند خواندن آن سخت است، ولی در واقع دقیقاً همان الگوریتم zk را اجرا میکند.
قرارداد cTornado.sol توکن حاکمیتی تورنادو کش (Tornado Cash) با استاندارد ERC20 است. این قرارداد جزو پروتکل اصلی نیست و صرفاً برای رایگیری و تصمیمگیری حاکمیتی استفاده میشود.
جاهایی که تورنادو کش (Tornado Cash) میتواند در مصرف گس بهینه تر عمل کند
با اینکه معماری Tornado Cash بسیار حرفهای طراحی شده، ولی چند فرصت مشخص برای کاهش مصرف گس (Gas Optimization) وجود دارد:
- تورنادو کش (Tornado Cash) برای یافتن زیردرختهای Merkle از پیشمحاسبهشده (که فقط شامل صفر هستند) از جستوجوی خطی استفاده میکند. این عملیات میتواند با استفاده از یک جستوجوی دودویی (binary search) از پیش کدنویسیشده بهشدت سریعتر شود و گس کمتری مصرف کند.
- در چند بخش از کد، متغیرهایی که روی استک قرار دارند از نوع
uint32تعریف شدهاند. اما چون ماشین مجازی اتریوم (EVM) باuint256کار میکند، هنگام استفاده از این متغیرها نیاز به تبدیل ضمنی (implicit casting) است که گس مصرف میکند. استفاده مستقیم ازuint256میتواند این هزینه را حذف کند. - برخی مقادیر
constantبهصورتpublicتعریف شدهاند، در حالیکه هیچ قرارداد دیگری آنها را نمیخواند. تعریف عمومی برایconstantها تنها زمانی مفید است که قرارداد دیگری قرار باشد آنها را بخواند. در غیر این صورت، فقط باعث افزایش حجم بایتکد و مصرف گس هنگام دیپلوی میشود. - در بسیاری از حلقهها از
i++استفاده شده، در حالیکه++iاندکی کممصرفتر است چون یک عملیات کمتری دارد (در EVM). این تغییر ساده، بدون تأثیر روی منطق، در قراردادهایی با حلقههای تکرارشونده میتواند در مجموع مصرف گس را کاهش دهد. - مقدار
nullifierHashesهم بهعنوان یکpublic mappingوجود دارد و هم تابعisSpent()برای دسترسی به آن تعریف شده. از آنجا کهpublic mappingبهطور خودکار یک getter داخلی میسازد، تابعisSpent()اضافه و غیرضروری است و فقط باعث افزایش حجم قرارداد میشود.
نتیجه گیری
و به این ترتیب، به پایان رسیدیم؛ ما کل کدهای تورنادو کش (Tornado Cash) را مرور کردیم و درک خوبی از عملکرد هر متغیر و تابع بهدست آوردیم. Tornado Cash با وجود داشتن کدی نسبتاً کوچک، میزان قابل توجهی از پیچیدگی و منطق پیشرفته را در خود جای داده است. در این مسیر با چند تکنیک غیر بدیهی و سطح بالا آشنا شدیم، از جمله:
- استفاده از اثباتهای دانش صفر (Zero Knowledge Proofs)
- استفاده از درخت Merkle افزایشی (Incremental Merkle Tree)
- پیاده سازی تابع هش سفارشی از طریق بایتکد خام (Raw Bytecode)
- درک مکانیزم nullifierها
- نحوه برداشت ناشناس وجوه
- مکانیزم جلوگیری از frontrunning در dappهای مبتنی بر zk-proof
راستی! برای دریافت مطالب جدید در کانال تلگرام یا پیج اینستاگرام سورس باران عضو شوید.
- انتشار: ۸ مرداد ۱۴۰۴
دسته بندی موضوعات
- آموزش ارز دیجیتال
- آموزش برنامه نویسی
- آموزش متنی برنامه نویسی
- اطلاعیه و سایر مطالب
- پروژه برنامه نویسی
- دوره های تخصصی برنامه نویسی
- رپورتاژ
- فیلم های آموزشی
- ++C
- ADO.NET
- Adobe Flash
- Ajax
- AngularJS
- apache
- ARM
- Asp.Net
- ASP.NET MVC
- AVR
- Bootstrap
- CCNA
- CCNP
- CMD
- CSS
- Dreameaver
- EntityFramework
- HTML
- IOS
- jquery
- Linq
- Mysql
- Oracle
- PHP
- PHPMyAdmin
- Rational Rose
- silver light
- SQL Server
- Stimulsoft Reports
- Telerik
- UML
- VB.NET&VB6
- WPF
- Xml
- آموزش های پروژه محور
- اتوکد
- الگوریتم تقریبی
- امنیت
- اندروید
- اندروید استودیو
- بک ترک
- بیسیک فور اندروید
- پایتون
- جاوا
- جاوا اسکریپت
- جوملا
- دلفی
- دوره آموزش Go
- دوره های رایگان پیشنهادی
- زامارین
- سئو
- ساخت CMS
- سی شارپ
- شبکه و مجازی سازی
- طراحی الگوریتم
- طراحی بازی
- طراحی وب
- فتوشاپ
- فریم ورک codeigniter
- فلاتر
- کانستراکت
- کریستال ریپورت
- لاراول
- معماری کامپیوتر
- مهندسی اینترنت
- هوش مصنوعی
- یونیتی
- کتاب های آموزشی
- Android
- ASP.NET
- AVR
- LINQ
- php
- Workflow
- اچ تی ام ال
- بانک اطلاعاتی
- برنامه نویسی سوکت
- برنامه نویسی موبایل
- پاسکال
- پایان نامه
- پایتون
- جاوا
- جاوا اسکریپت
- جی کوئری
- داده کاوی
- دلفی
- رباتیک
- سئو
- سایر کتاب ها
- سخت افزار
- سی اس اس
- سی پلاس پلاس
- سی شارپ
- طراحی الگوریتم
- فتوشاپ
- مقاله
- مهندسی نرم افزار
- هک و امنیت
- هوش مصنوعی
- ویژوال بیسیک
- نرم افزار و ابزار برنامه نویسی
- وردپرس