در ساختار درخت مرکل، زمانی که یک نود میانی به جای یک برگ به سیستم معرفی میشود، احتمال بروز حملهای به نام Second Preimage وجود دارد.
نام این حمله ممکن است گمراهکننده باشد، زیرا بهاشتباه این تصور را ایجاد میکند که تابع هش مورد استفاده میتواند چندین تصویر قابل محاسبه داشته باشد. اما در واقع، توابع هش مدرن چنین ضعفی ندارند و امکان یافتن دو ورودی متفاوت با هش یکسان، عملاً وجود ندارد.
نام دقیقتری که برای این نوع حمله میتوان بهکار برد، “حمله نود بهجای برگ” یا “حمله اثبات کوتاهشده” است. این نامها بهدرستی نشان میدهند که مهاجم چگونه با ارائه یک نود میانی بهعنوان برگ، فرآیند تأیید را دور میزند.
پیشنیازها
در این مقاله، فرض میکنیم خواننده با مفاهیم درخت مرکل و اثبات مرکل آشنا است.
نمادگذاری
در اینجا، h(x) نشاندهنده هش مقدار x است و h(x + y) هش ترکیب مقادیر x و y را نشان میدهد. ما از تابع keccak256 بهعنوان مرجع استفاده میکنیم تا مفاهیم بعدی را سادهتر بیان کنیم. البته تمام ایدههای مطرحشده برای سایر توابع هش نیز قابل اجرا هستند.
برای نمایش برگهای درخت مرکل از نماد ℓ استفاده میکنیم و برگ شماره i را با ℓᵢ نشان میدهیم.
نمونهای از یک حمله Second Preimage در درخت مرکل سالیدیتی
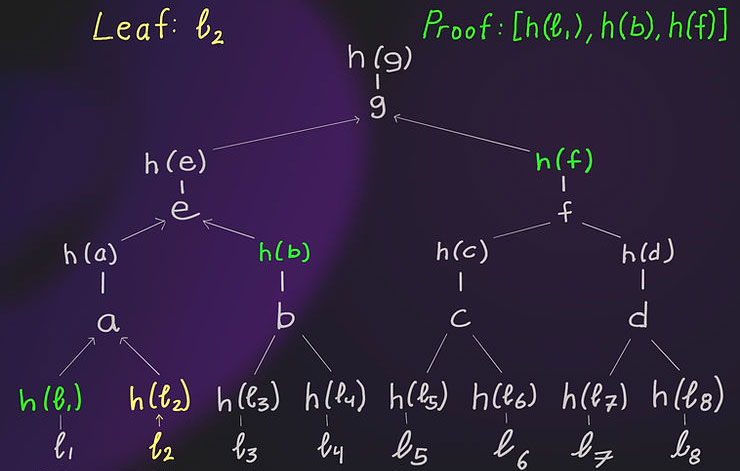
فرض کنید میخواهیم برای برگ شماره ۲ (ℓ₂) درخت مرکل زیر، یک اثبات (Merkle Proof) ایجاد کنیم. در این حالت، مقدار برگ ℓ₂ است و مسیر اثبات شامل مقادیر [h(ℓ₁), h(b), h(f)] خواهد بود. مقادیر a، b، c تا g همگی حاصل ترکیب مقادیر فرزندان خود هستند (یعنی a برابر است با h(ℓ₁ + ℓ₂) و به همین ترتیب).
در اینجا، زمانی اثبات را معتبر تلقی میکنیم که مقدار نهایی h(g) برابر با ریشه مرکل (Merkle Root) باشد.
در این سناریو، مسیر اثباتی که برای ℓ₂ ارائه میدهیم شامل سه مقدار [h(ℓ₁), h(b), h(f)] است که در نمودار با رنگ سبز مشخص شدهاند. این سه مقدار برای بازسازی مسیر تا ریشه استفاده میشوند:
|
1 2 3 |
h(a) = h(h(ℓ₁) + h(ℓ₂)) h(e) = h(h(a) + h(b)) h(g) = h(h(e) + h(f)) |
h(g) با مقدار ریشه درخت مرکل برابر باشد، اثبات پذیرفته میشود:|
1 |
return root == h(g) |
حمله Second Preimage چگونه کار میکند؟
فرض کنید مهاجم بهجای یک برگ واقعی، مقدار a را بهعنوان برگ ارائه دهد و مسیر اثبات را نیز برابر با [h(b), h(f)] قرار دهد.
در این حالت، قرارداد هوشمند مقدار a را بهعنوان برگ دریافت میکند، در حالی که a = h(h(ℓ₁), h(ℓ₂)) است. یعنی a در واقع یک نود میانی از درخت مرکل است، نه یک برگ واقعی.
نکته کلیدی اینجاست: اگر یک اثبات مرکل معتبر باشد، مهاجم میتواند نسخه کوتاهتری از همان اثبات را هم معتبر جلوه دهد، بهشرط آنکه مقدار اول مسیر اثبات (که در اصل بخشی از نود والد بوده) را بهجای برگ اصلی به قرارداد بدهد.
به عبارت دیگر، مهاجم با ارائه یک نود میانی بهعنوان برگ، و استفاده از بخشی از اثبات قبلی، موفق میشود سیستم را فریب دهد.
در نتیجه، قرارداد هوشمند اثباتی را تأیید میکند که برگ آن اصلاً در درخت مرکل اصلی وجود ندارد!
چطور میتوانیم جلوی این حمله را بگیریم؟
هشدار OpenZeppelin درباره حمله Second Preimage
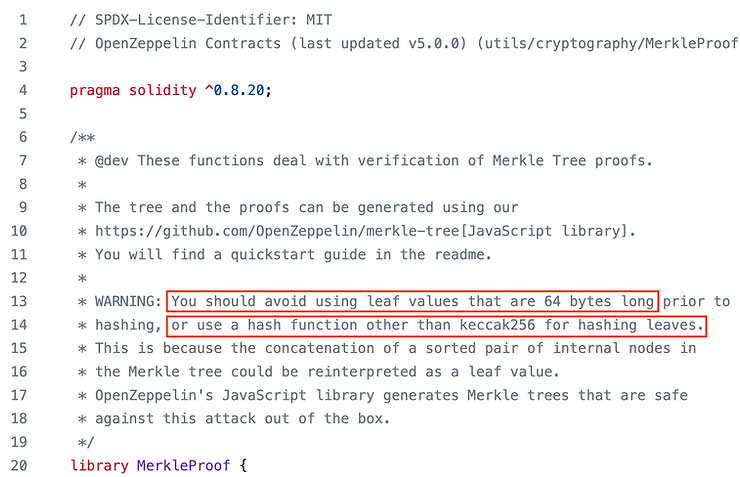
کتابخانه درخت مرکل (Merkle Tree) در مجموعه ابزارهای OpenZeppelin، بهدرستی در بخش توضیحات (کامنت ها) نسبت به این حمله هشدار داده است. این هشدار همراه با چند راهکار پیشنهادی ارائه شده که هدف آنها جلوگیری از اجرای موفقیتآمیز چنین حملهای در قراردادهای هوشمند است.
در ادامه، به بررسی دقیق این راهکارها میپردازیم و توضیح میدهیم که چگونه هر یک از آنها میتوانند از وقوع این نوع حمله جلوگیری کنند.
این حمله به برگهای ۶۴ بایتی نیاز دارد
برای اجرای موفقیتآمیز این نوع حمله، مهاجم باید تصویر اولیه (preimage) یک نود میانی را بهعنوان برگ به قرارداد ارائه دهد. نه صرفاً هش آن نود. بهعبارت دقیقتر، مهاجم باید مقدار a را بهعنوان برگ وارد کند، نه h(a).
از آنجا که در سالیدیتی هش ها بهصورت پیشفرض ۳۲ بایتی هستند، مقدار a = h(ℓ₁) + h(ℓ₂) یک رشته ۶۴ بایتی خواهد بود (ترکیب دو هش ۳۲ بایتی). بنابراین اگر قرارداد هوشمند ورودیهای ۶۴ بایتی را بهعنوان برگ نپذیرد، این حمله قابل اجرا نخواهد بود.
در نتیجه اگر طول ورودیهای برگ متفاوت از ۶۴ بایت باشد، مهاجم نمیتواند مقدار h(ℓ₁) + h(ℓ₂) را بهعنوان یک برگ جعلی وارد کند و در نتیجه امکان اجرای حمله از بین میرود.
استفاده از تابع هش متفاوت برای برگ ها بهعنوان راهکار دفاعی
در برخی کاربردها، ممکن است نیاز داشته باشیم که قرارداد برگ های ۶۴ بایتی را بپذیرد. در این شرایط، نمیتوان صرفاً با محدود کردن طول ورودی، جلوی حمله را گرفت. اما همچنان راهی برای مقابله وجود دارد: استفاده از تابع هش متفاوت برای برگ ها نسبت به آنچه در مسیر اثبات و محاسبه ریشه استفاده میشود.
بهعبارت سادهتر، زمانی که برگ ها را هش میکنیم، از تابعی مانند h' استفاده میکنیم، در حالی که برای بقیه نودهای درخت از تابع معمول h استفاده میکنیم. این کار باعث میشود مهاجم نتواند یک نود میانی را با عبور از همان مسیر هش، بازسازی و بهعنوان برگ جعلی معرفی کند.
برای مثال، مهاجم قصد دارد مقدار a = h(h(ℓ₁), h(ℓ₂)) را بهعنوان برگ وارد کند تا اثبات تقلبی را ایجاد کند. اما اگر سیستم، برگها را ابتدا از طریق تابع دیگری مانند h'(x) هش کرده باشد، آنگاه مهاجم دیگر نمیتواند از مسیر اصلی h(a) برای ساختن این برگ استفاده کند. چون هش اولیه برگ متفاوت خواهد بود.
استفاده OpenZeppelin از هش دوتایی بهعنوان “تابع هش متفاوت”
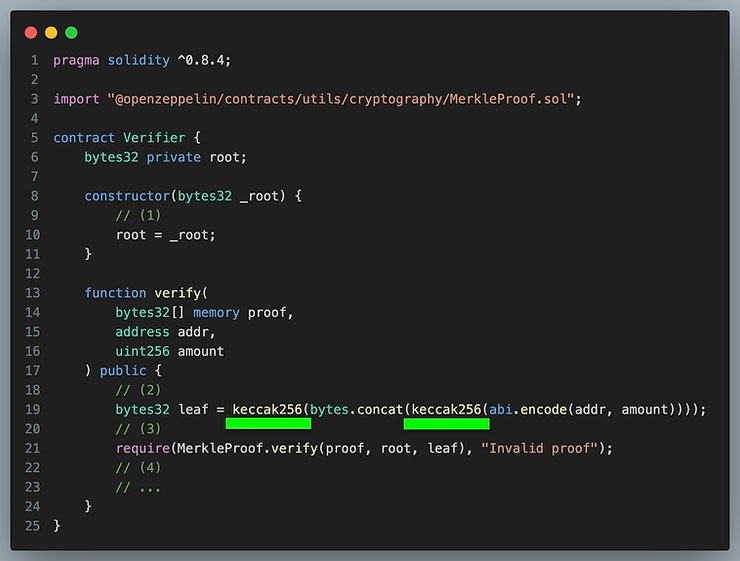
کتابخانه OpenZeppelin برای تفکیک بین هش برگها و نودهای میانی، بهجای استفاده از تابع هش متفاوت و پرهزینه (مانند توابع پیشکامپایلشده)، از یک راهکار ساده و مؤثر بهره میبرد: اعمال هش دوباره روی داده برگ. بهعبارت دیگر، اگر تابع هش معمول را h(x) در نظر بگیریم، آنگاه هش برگها بهصورت h'(x) = h(h(x)) محاسبه میشود.
ما با زیرخط های سبز مشخص کردهایم که در چه بخشهایی، هش دوبار روی داده اولیه اعمال شده تا برگ نهایی در درخت ساخته شود.
توجه داشته باشید که این کتابخانه شما را ملزم نمیکند که حتماً هش را دوبار اعمال کنید. در واقع حتی شما را مجبور به هشکردن برگ ها هم نمیکند! اما اگر برگ ها را اصلاً هش نکنید، ممکن است مسیر حمله هایی فراتر از حمله second preimage باز شود.
جمع بندی
حمله Second Preimage در درخت مرکل سالدیتی زمانی قابل اجرا است که بتوان نسخه کوتاهشدهای از یک اثبات معتبر را ارائه داد و همچنان ریشه مرکل (Merkle Root) را بازسازی کرد. درخت مرکل فقط یک تصویر اولیه (preimage) دارد، اما این ریشه بهصورت مرحلهای و تدریجی ساخته میشود، نه از طریق هشکردن کل مسیر اثبات بهصورت یکجا. به همین دلیل، اگر اثبات را از نقطهای جلوتر در دنباله آغاز کنیم، ممکن است بتوانیم ورودی متفاوتی ارائه دهیم که همان ریشه را تولید میکند. درک دقیق این ساختار برای توسعه قراردادهای ایمن ضروری است. به ویژه افرادی که در مسیر آموزش برنامه نویسی بلاکچین و امنیت آن فعالیت میکنند.
خبر خوب این است که مقابله با این حمله بسیار ساده است: کافی است اطمینان حاصل کنیم که هیچ مقدار میانی در درخت مرکل بهاشتباه بهعنوان یک برگ (leaf) تفسیر نشود. بهعبارت دیگر، تنها مقادیری که واقعاً برگ هستند باید بهعنوان برگ معتبر در ورودی پذیرفته شوند.
راستی! برای دریافت مطالب جدید در کانال تلگرام یا پیج اینستاگرام سورس باران عضو شوید.
- انتشار: ۶ مرداد ۱۴۰۴
دسته بندی موضوعات
- آموزش ارز دیجیتال
- آموزش برنامه نویسی
- آموزش متنی برنامه نویسی
- اطلاعیه و سایر مطالب
- پروژه برنامه نویسی
- دوره های تخصصی برنامه نویسی
- رپورتاژ
- فیلم های آموزشی
- ++C
- ADO.NET
- Adobe Flash
- Ajax
- AngularJS
- apache
- ARM
- Asp.Net
- ASP.NET MVC
- AVR
- Bootstrap
- CCNA
- CCNP
- CMD
- CSS
- Dreameaver
- EntityFramework
- HTML
- IOS
- jquery
- Linq
- Mysql
- Oracle
- PHP
- PHPMyAdmin
- Rational Rose
- silver light
- SQL Server
- Stimulsoft Reports
- Telerik
- UML
- VB.NET&VB6
- WPF
- Xml
- آموزش های پروژه محور
- اتوکد
- الگوریتم تقریبی
- امنیت
- اندروید
- اندروید استودیو
- بک ترک
- بیسیک فور اندروید
- پایتون
- جاوا
- جاوا اسکریپت
- جوملا
- دلفی
- دوره آموزش Go
- دوره های رایگان پیشنهادی
- زامارین
- سئو
- ساخت CMS
- سی شارپ
- شبکه و مجازی سازی
- طراحی الگوریتم
- طراحی بازی
- طراحی وب
- فتوشاپ
- فریم ورک codeigniter
- فلاتر
- کانستراکت
- کریستال ریپورت
- لاراول
- معماری کامپیوتر
- مهندسی اینترنت
- هوش مصنوعی
- یونیتی
- کتاب های آموزشی
- Android
- ASP.NET
- AVR
- LINQ
- php
- Workflow
- اچ تی ام ال
- بانک اطلاعاتی
- برنامه نویسی سوکت
- برنامه نویسی موبایل
- پاسکال
- پایان نامه
- پایتون
- جاوا
- جاوا اسکریپت
- جی کوئری
- داده کاوی
- دلفی
- رباتیک
- سئو
- سایر کتاب ها
- سخت افزار
- سی اس اس
- سی پلاس پلاس
- سی شارپ
- طراحی الگوریتم
- فتوشاپ
- مقاله
- مهندسی نرم افزار
- هک و امنیت
- هوش مصنوعی
- ویژوال بیسیک
- نرم افزار و ابزار برنامه نویسی
- وردپرس