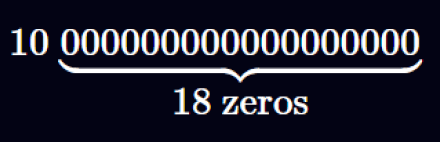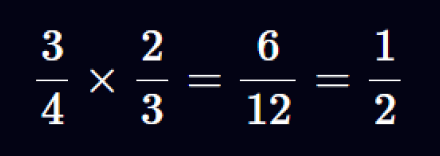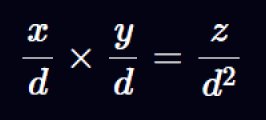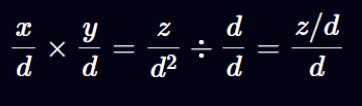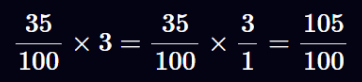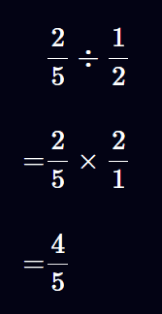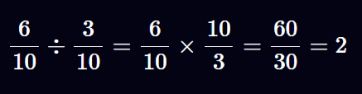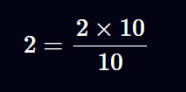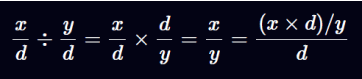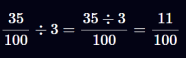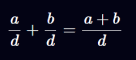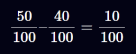آموزش محاسبات اعشاری ثابت در سالیدیتی + مثال

0 دیدگاه

در سالیدیتی، وقتی می‌خواهیم اعداد کسری را ذخیره کنیم، از نوعی عدد صحیح استفاده می‌کنیم که فقط صورت کسر را نگه می‌دارد. مخرج کسر به صورت ضمنی وجود دارد و معمولاً مقدار ثابتی مثل 10^{18} دارد. این روش بخشی از مفهومی است که با عنوان محاسبات اعشاری ثابت در سالیدیتی شناخته می‌شود و در بسیاری از قراردادهای هوشمند کاربرد حیاتی دارد.

در اکثر زبان های برنامه نویسی، به این نوع محاسبه نیازی نیست چون آن زبان ها از اعداد اعشاری متحرک (floating point numbers) پشتیبانی می‌کنند. اما سالیدیتی فقط اعداد صحیح را ارائه می‌دهد، و توسعه دهندگان مجبور هستند از روش‌های جایگزین برای کار با مقادیر کسری استفاده کنند.

قراردادهای هوشمند حوزه DeFi تقریباً همیشه از این نوع اعداد استفاده می‌کنند. به همین دلیل، اگر می‌خواهید در این حوزه فعالیت کنید، باید درک درستی از محاسبات اعشاری ثابت داشته باشید.

برای مثال، وقتی مخرج ضمنی را در نظر بگیریم، عدد ثابت “10” به معنای مقدار 0.1 خواهد بود.

چرا عدد 10^{18} در سالیدیتی اهمیت دارد؟

رایج‌ترین نوع عدد اعشاری ثابت در سالیدیتی عددی با مخرج 10^{18} است. این همان تعداد اعشاری (decimals) است که اتریوم و بیشتر توکن های ERC-20 از آن استفاده می‌کنند. وقتی موجودی یک آدرس را می‌خوانید، باید بدانید که آن عدد به صورت ضمنی تقسیم بر 10^{18} شده است. مثلاً اگر موجودی برابر با 10^{19} باشد، به معنای ۱۰ اتر خواهد بود.

عدد اعشاری ثابتی با مخرج 10^{18} آن‌قدر متداول است که توسعه دهندگان سالیدیتی در جامعه فنی این حوزه، آن را با اصطلاح “Wad” می‌شناسند؛ اصطلاحی که نخستین بار توسط پروژه MakerDAO مطرح شد. در بسیاری از مواقع، عدد اعشاری ۱۸ رقمی به‌گونه‌ای در نظر گرفته می‌شود که ۱۸ رقم سمت راست آن مربوط به بخش اعشار است. برای نمونه، عدد “10” در این قالب به این صورت نمایش داده می‌شود:

با این حال، ما متوجه شده‌ایم که این مدل ذهنی که ۱۸ رقم سمت راست را به عنوان بخش اعشاری در نظر می‌گیرد، یادگیری محاسبات اعشاری ثابت را دشوارتر می‌کند. به همین دلیل، در این مقاله از یک مدل ذهنی ساده‌تر استفاده می‌کنیم: عدد اعشاری ثابت فقط صورت کسر را نگه می‌دارد و همیشه مخرج را به صورت ضمنی 10^{18} در نظر می‌گیریم.

تبدیل عدد صحیح به عدد اعشاری ثابت

برای تبدیل یک عدد صحیح به عدد اعشاری ثابت، کافی است آن را در مخرج ضمنی ضرب کنید. به عنوان نمونه، مقدار “۲ اتر” برابر با عدد صحیحی در مقیاس 10^{18} است. بنابراین برای تبدیل عدد صحیح ۲ به مقدار “۲ اتر”، عدد ۲ را در 10^{18} ضرب می‌کنیم. از آنجا که در ادامه محاسبات نیز مخرج 10^{18} به صورت ضمنی حضور دارد، این عامل در عمل حذف می‌شود و نتیجه‌ نهایی دقیقاً با مقیاس مورد نظر تطابق خواهد داشت.

ضرب دو عدد اعشاری ثابت

برای ضرب دو عدد اعشاری ثابت، باید قواعد ضرب کسرها را دنبال کنیم:

صورت‌ها (numerators) را در یکدیگر ضرب می‌کنیم
مخرج‌ها (denominators) را نیز در یکدیگر ضرب می‌کنیم
حاصل را ساده می‌کنیم

برای مثال:

با این حال، می‌توان این محاسبه را در عمل بهینه‌سازی کرد، چرا که در اعداد اعشاری ثابت، مخرج همیشه مقدار ثابتی دارد و تغییر نمی‌کند.

اکنون اجازه دهید مجموعه‌ای دیگر از کسرها را بررسی کنیم که همگی دارای یک مخرج مشترک هستند:

با این حال، نمی‌خواهیم عددی را بازگردانیم که مخرج ضمنی آن برابر با باشد، زیرا این مقدار با مخرج ثابتی که در ابتدا انتخاب کرده‌ایم سازگاری ندارد. بنابراین، باید صورت و مخرج کسر حاصل را بر تقسیم کنیم تا نتیجه نهایی با مخرج ضمنی مورد نظرمان هم‌راستا باقی بماند و در قالب یک عدد اعشاری ثابت استاندارد قرار گیرد.

بنابراین، اگر $x$ و $y$ دو عدد اعشاری ثابت باشند که مخرج ضمنی آن‌ها برابر با d^2 است، می‌توان حاصل ضرب آن‌ها را با استفاده از فرمول (x \times y)/d محاسبه کرد.

مثال کدنویسی برای ضرب اعداد اعشاری ثابت

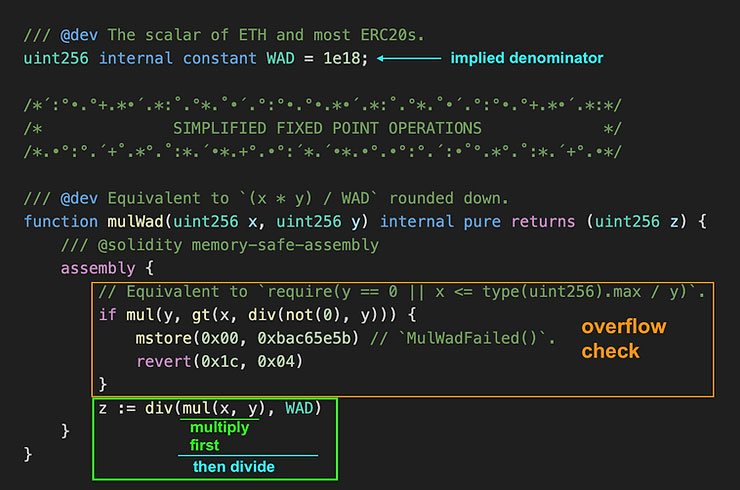
کتابخانه Solady تابعی به نام mulWad ارائه می‌دهد که برای ضرب دو عدد اعشاری ثابت با مخرج ضمنی Wad (یعنی 10^{18}) طراحی شده است. در ادامه، کد مربوط به این تابع را مشاهده می‌کنید و پس از آن، توضیح می‌دهیم که این کد چگونه با مفاهیم مطرح‌شده در بخش‌های قبل ارتباط دارد:

الگوریتم اصلی در پایین تصویر (داخل کادر سبز) قرار دارد. در این بخش، محاسبه (x \times y)/d انجام می‌شود؛ جایی که $d$ همان مقدار WAD یا 10^{18} است (همان‌طور که در بالای تصویر محل تعریف WAD نمایش داده شده است).

مثال دنیای واقعی

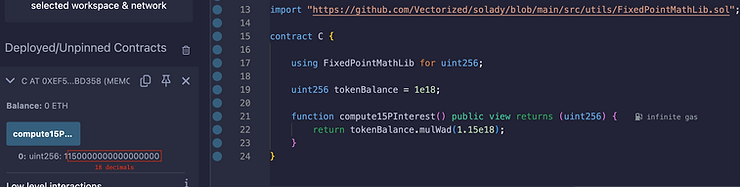
فرض کنید یک کاربر ۱ DAI دارد (که دارای ۱۸ رقم اعشار است) و می‌خواهیم موجودی او را با فرض دریافت ۱۵٪ سود محاسبه کنیم. این یک مثال واضح از نیاز به محاسبات اعشاری ثابت است، چون در سالیدیتی نمی‌توانیم مستقیماً عددی را در ۱.۱۵ ضرب کنیم.

خروجی برابر با ۱.۱۵ است پس از تقسیم بر 1e18. البته، نمی‌توانیم واقعاً بر 1e18 تقسیم کنیم، چون این کار اعشار را از بین می‌برد. ما به یک نمایش اعشاری ثابت نیاز داریم، چون عدد ۱.۱۵ را نمی‌توان به‌صورت عدد صحیح نمایش داد. کد بالا را می‌توان در Remix تست کرد.

ضرب یک عدد اعشاری ثابت در یک عدد صحیح

ضرب یک کسر x در یک عدد صحیح y معادل است با ضرب در y/1:

بنابراین، زمانی که یک عدد اعشاری ثابت را در یک عدد صحیح ضرب می‌کنیم، نیازی به انجام مراحل اضافی نداریم. کافی است حاصل ضرب را به‌عنوان یک عدد اعشاری ثابت تفسیر کنیم، در حالی که مخرج آن بدون تغییر باقی می‌ماند.

تقسیم اعداد اعشاری ثابت

برای تقسیم دو کسر، کسر دوم را وارونه می‌کنیم و سپس آن‌ها را در یکدیگر ضرب می‌کنیم. به عنوان مثال:

اکنون بیایید مثالی را بررسی کنیم که هر دو کسر دارای مخرج یکسان هستند:

توجه داشته باشید که مخرج مشترک ۱۰ در محاسبه حذف شد. اگر بخواهیم عدد ۲ را با مخرج ضمنی ۱۰ نمایش دهیم (یعنی به عنوان یک عدد اعشاری ثابت با مخرج ۱۰)، باید دوباره آن را در ۱۰ ضرب کنیم:

بنابراین، اگر دو عدد عمومی x و y دارای مخرج مشترک باشند و بخواهیم خروجی را نیز با مخرج ضمنی نمایش دهیم، باید مراحل زیر را انجام دهیم:

بنابراین، اگر و $y$ دو عدد اعشاری ثابت با مخرج ضمنی $d$ باشند، می‌توان خارج‌قسمت آن‌ها را با فرمول (x \times d)/y محاسبه کرد.

/// @dev Equivalent to `(x * WAD) / y` rounded down.
function divWad(uint256 x, uint256 y) internal pure returns (uint256 z) {
    /// @solidity memory-safe-assembly
    assembly {
        // Equivalent to `require((y != 0 && (WAD == 0 || x <= type(uint256).max / WAD))`.
        if iszero(mul(y, iszero(mul(WAD, gt(x, div(not(0), WAD)))))) {
            mstore(0x00, 0x7c5f487d) // `DivWadFailed()`.
            revert(0x1c, 0x04)
        }
        z := div(mul(x, WAD), y)
    }
}

/// @dev Equivalent to `(x * WAD) / y` rounded down.

function divWad(uint256 x, uint256 y) internal pure returns (uint256 z) {

/// @solidity memory-safe-assembly

assembly {

// Equivalent to `require((y != 0 && (WAD == 0 || x <= type(uint256).max / WAD))`.

if iszero(mul(y, iszero(mul(WAD, gt(x, div(not(0), WAD)))))) {

mstore(0x00, 0x7c5f487d) // `DivWadFailed()`.

revert(0x1c, 0x04)

}

z := div(mul(x, WAD), y)

}

اگر توابع mulWad() و divWad() را در کنار هم قرار دهیم، می‌بینیم که تنها تفاوت بین آن‌ها (در مرحله محاسبه، نه بررسی سرریز) این است که در حالت تقسیم (divWad)، ضرب در یک کسر وارونه انجام می‌شود.

تقسیم یک عدد اعشاری ثابت بر یک عدد صحیح

فرض کنید می‌خواهیم عدد ۲.۵ را بر ۲ تقسیم کنیم (یا به‌طور کلی، یک کسر را بر یک عدد صحیح تقسیم کنیم). نیازی نیست که عدد ۲ را با فرمول (2 \times d)/d به یک عدد اعشاری ثابت تبدیل کنیم.

تقسیم یک کسر $x$ بر یک عدد صحیح $y$ ، معادل این است که صورت کسر $x$ را بر تقسیم کنیم.

توجه داشته باشید که حاصل 35 \ div 3 برابر با ۱۱ است، نه ۱۱.۶۶۶، زیرا در اینجا از تقسیم صحیح (integer division) استفاده می‌کنیم، نه از اعداد اعشاری متحرک (floating point). در این حالت، عدد اعشاری ثابت را مستقیماً بر عدد صحیح تقسیم می‌کنیم و نتیجه را به‌عنوان یک عدد اعشاری ثابت تفسیر می‌کنیم. همانند ضرب یک عدد اعشاری ثابت در عدد صحیح، مخرج نیز بدون تغییر باقی می‌ماند.

جمع و تفریق اعداد اعشاری ثابت

برای جمع و تفریق کسرهایی که مخرج یکسان دارند، کافی است صورت‌ها را با هم جمع یا از هم کم کنیم و مخرج را نادیده بگیریم. نتیجه به‌عنوان یک عدد اعشاری ثابت با همان مخرج ضمنی که جمع‌شونده‌ها یا تفریق‌شونده‌ها داشتند، تفسیر می‌شود. برای مثال:

بنابراین، هنگام جمع کردن اعداد اعشاری ثابت با مخرج یکسان، کافی است آن‌ها را مانند اعداد صحیح معمولی با هم جمع کنیم.

به عنوان مثال، فرض کنید مخرج ضمنی برابر با ۱۰۰ باشد:

برای محاسبه، کافی است 50 – 40 = 10 را انجام دهیم؛ نیازی نیست عدد ۱۰۰ را وارد محاسبه کنیم.

عدد اعشاری ثابت دودویی در مقابل ده‌دهی

عدد اعشاری ثابت دودویی (Binary Fixed Point Number) عددی است که مخرج آن به صورت توانی از ۲ نمایش داده می‌شود، یعنی به فرم 2^n. معمولاً برای نمایش این نوع اعداد از نمادگذاری Q استفاده می‌شود. به عنوان مثال، قالب UQ112x112 از 2^{112} به عنوان مخرج ضمنی استفاده می‌کند. حرف U نشان‌دهنده “بدون علامت بودن” (unsigned) عدد است. نوع داده‌ای که برای نگهداری مقدار در قالب UQ112x112 به کار می‌رود، عدد صحیح ۲۲۴ بیتی است. به بیان دیگر، ۱۱۲ بیت سمت راست برای نمایش قسمت اعشاری و ۱۱۲ بیت سمت چپ برای نمایش قسمت صحیح به‌کار می‌رود.

مثال دیگر، قالب UQ64x64 (یا UQ64.64) است که از نوع داده uint128 استفاده می‌کند. در این قالب، ۶۴ بیت کم‌ارزش‌تر (least significant) مربوط به بخش اعشاری و ۶۴ بیت پرارزش‌تر (most significant) مربوط به بخش صحیح عدد هستند. این قالب را هم می‌توان به‌صورت عددی با مخرج ضمنی 2^{64} تفسیر کرد، همان‌طور که در ادامه خواهیم دید.

مزیت استفاده از عدد اعشاری ثابت دودویی این است که هنگام تبدیل یک عدد صحیح به عدد اعشاری ثابت، به‌جای ضرب در مخرج می‌توان از جابجایی بیت به چپ (left bit shift) استفاده کرد که از نظر مصرف گس بسیار به‌صرفه‌تر است. در عملیات تقسیم نیز می‌توان به‌جای تقسیم، از جابجایی بیت به راست استفاده کرد.

به عنوان یک مثال ساده، در نظر بگیرید که:

عدد ۲ در مبنای دودویی برابر با 10 است
عدد ۱۶ در مبنای دودویی برابر با 10000 است
عدد ۱۶ برابر است با 16 = 2 \times 2^3، و معادل است با: binary(1000) = binary(10) << 3

توجه داشته باشید که عدد ۳، در بند (۳) به‌عنوان توان ظاهر شده و در همان بند، مقدار جابجایی بیت به چپ در عبارت (۴) نیز همین عدد است.

رابطه بین جابجایی بیت به اندازه و ضرب در 2^e، یک قاعده کلی محسوب می‌شود. عملیات‌های زیر از نظر نتیجه معادل هستند:

// x * 2¹¹² equals x left bitshifted by 112 bits
x * 2 ** 112 == x << 112

// x / 2¹¹² equals x right bitshifted by 112 bits
x / 2 ** 112 == x >> 112

// x * 2¹¹² equals x left bitshifted by 112 bits

x * 2 ** 112 == x << 112

// x / 2¹¹² equals x right bitshifted by 112 bits

x / 2 ** 112 == x >> 112

مقدار $x$ می‌تواند هر عدد دلخواهی باشد، به شرطی که در محدوده نوع داده عدد صحیح بدون علامت (unsigned integer) قرار بگیرد.

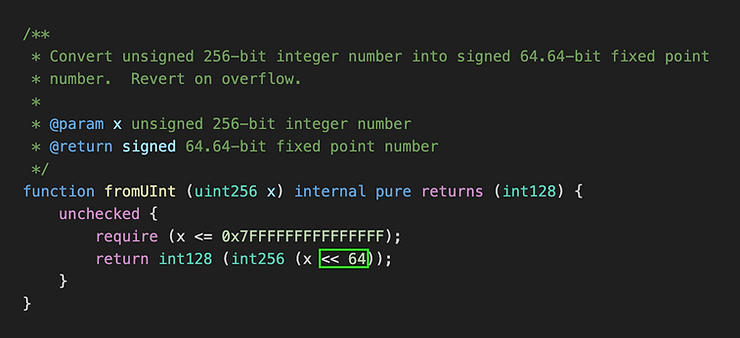
کتابخانه ABDK برای تبدیل اعداد صحیح بدون علامت به اعداد اعشاری ثابت (با مخرج ضمنی 2^{64}) از تابع زیر استفاده می‌کند:

دستور require اطمینان حاصل می‌کند که مقدار از بیشینه مقدار نوع int64 کمتر باشد، زیرا کتابخانه ABDK از اعداد اعشاری ثابت علامت‌دار استفاده می‌کند. جابجایی بیت به چپ به اندازه ۶۴ بیت معادل است با ضرب در 2^{64}.

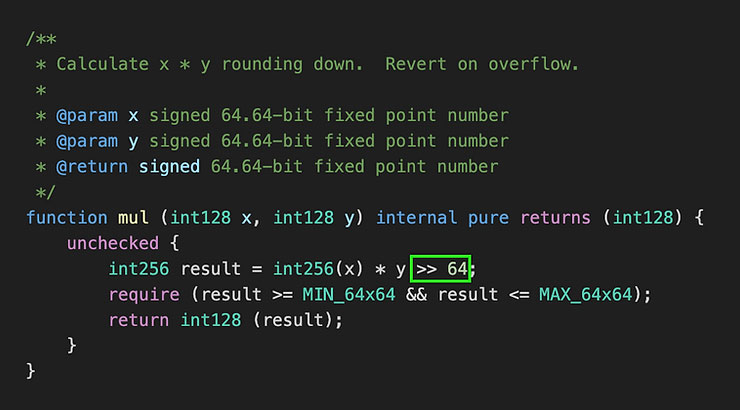
به‌صورت مشابه، زمانی که کتابخانه ABDK عمل ضرب را انجام می‌دهد، به‌جای تقسیم حاصل‌ضرب و بر 2^{64}، یک جابجایی بیت به راست به اندازه ۶۴ بیت انجام می‌دهد:

کتابخانه اعداد اعشاری ثابت در Uniswap V2

کتابخانه مربوط به اعداد اعشاری ثابت در نسخه دوم Uniswap ساختار بسیار ساده‌ای دارد، زیرا تنها عملیاتی که Uniswap V2 با این نوع اعداد انجام می‌دهد، جمع و تقسیم یک عدد اعشاری ثابت بر یک عدد صحیح است.

pragma solidity =0.5.16;

// A library for handling binary fixed point numbers (https://en.wikipedia.org/wiki/Q_(number_format))

// range: [0, 2**112 - 1]
// resolution: 1 / 2**112

library UQ112x112 {
    uint224 constant Q112 = 2**112;

    // encode a uint112 as a UQ112x112
    function encode(uint112 y) internal pure returns (uint224 z) {
        z = uint224(y) * Q112; // never overflows
    }

    // divide a UQ112x112 by a uint112, returning a UQ112x112
    function uqdiv(uint224 x, uint112 y) internal pure returns (uint224 z) {
        z = x / uint224(y);
    }
}

pragma solidity =0.5.16;

// A library for handling binary fixed point numbers (https://en.wikipedia.org/wiki/Q_(number_format))

// range: [0, 2**112 - 1]

// resolution: 1 / 2**112

library UQ112x112 {

uint224 constant Q112 = 2**112;

// encode a uint112 as a UQ112x112

function encode(uint112 y) internal pure returns (uint224 z) {

z = uint224(y) * Q112; // never overflows

}

// divide a UQ112x112 by a uint112, returning a UQ112x112

function uqdiv(uint224 x, uint112 y) internal pure returns (uint224 z) {

z = x / uint224(y);

}

تابع `encode()` در کتابخانه Uniswap V2

تابع encode() مقدار uint112 را به یک عدد اعشاری ثابت تبدیل می‌کند که در قالب uint224 ذخیره می‌شود. در Uniswap V2، مخرج ضمنی برای اعداد اعشاری ثابت برابر با 2**112 در نظر گرفته شده است. اگر به جای ضرب از شیفت بیت به چپ استفاده می‌شد، این عملیات می‌توانست از نظر مصرف گس بهینه‌تر باشد (احتمالاً این یک اشتباه از طرف توسعه‌دهندگان Uniswap بوده است).

عدد اعشاری ثابت در قالب uint224 ذخیره می‌شود، که دو برابر بزرگ‌تر از uint112 است و با آن تعامل دارد. در فرآیند رمزگذاری (encode)، بیت‌های عدد uint112 به طور مؤثر به ۱۱۲ بیت پرارزش‌تر (most significant bits) در uint224 منتقل می‌شوند.

برای درک بهتر عملکرد encode، می‌توان این فرآیند را با سایزهای کوچکتر uint شبیه‌سازی کرد. فرض کنید عدد اعشاری ثابتی با مخرج 2^8 داریم. در ادامه، نشان می‌دهیم وقتی یک عدد uint8 را به قالب اعشاری ثابت با مخرج 2^8 تبدیل می‌کنیم، چه اتفاقی می‌افتد:

با شروع از عدد ۱۲۵ که در مبنای دودویی به صورت 01111101 نمایش داده می‌شود، اگر آن را در 2^8 ضرب کنیم، حاصل برابر با ۳۲۰۰۰ خواهد بود. این عدد در قالب uint16 به شکل 0111110100000000 نمایش داده می‌شود. توجه داشته باشید که ضرب عدد ۱۲۵ در 2^8 دقیقاً همان اثری را دارد که جابجایی ۸ بیت به چپ.

تابع uqdiv() به‌سادگی عمل تقسیم یک عدد اعشاری ثابت بر یک عدد صحیح را انجام می‌دهد و نیازی به مراحل اضافی ندارد.

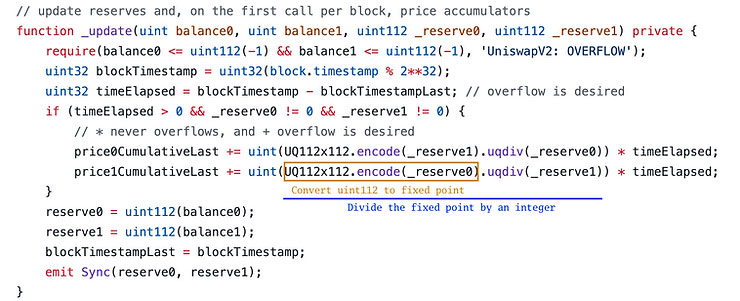
Uniswap از این کتابخانه برای تجمیع قیمت‌ها در اوراکل TWAP (میانگین قیمت وزنی بر حسب زمان) استفاده می‌کند. هر بار که یک به‌روزرسانی انجام می‌شود، قیمت جدید به یک متغیر انباشت‌گر افزوده می‌شود. این متغیر برای محاسبه میانگین قیمت با استفاده از مراحل اضافه‌تر (که خارج از محدوده این مقاله هستند) مورد استفاده قرار می‌گیرد. از آن‌جایی که قیمت‌ها به‌صورت کسر نمایش داده می‌شوند، استفاده از اعداد اعشاری ثابت بهترین راه‌حل برای نمایش آن‌ها محسوب می‌شود.

دو متغیر _reserve0 و _reserve1 مقادیر فعلی توکن‌های موجود در استخر را نگه می‌دارند و از نوع uint112 هستند. متغیرهای price0CumulativeLast و price1CumulativeLast از نوع UQ112x112 هستند (یعنی اعدادی اعشاری ثابت با مخرج ضمنی 2^{112}). در قطعه‌کد زیر از Uniswap V2، صورت کسر به عدد اعشاری ثابت (نوع UQ112x112) تبدیل شده و سپس بر یک عدد صحیح تقسیم می‌شود (مخرج به UQ112x112 تبدیل نمی‌شود). نتیجه نهایی، یک عدد اعشاری ثابت خواهد بود.

گرد کردن به بالا در مقابل گرد کردن به پایین

در بسیاری از کتابخانه‌های اعداد اعشاری ثابت، گزینه‌ای برای گرد کردن به بالا هنگام تقسیم وجود دارد. برای مثال، در کتابخانه Solady توابع زیر ارائه شده‌اند:

mulWadUp — دو عدد اعشاری ثابت را در یکدیگر ضرب می‌کند و هنگام تقسیم بر ، نتیجه را به بالا گرد می‌کند. به یاد داشته باشید که فرمول ضرب دو عدد اعشاری ثابت به صورت (x \times y) / d است.
mulDivUp — دو عدد اعشاری ثابت را تقسیم می‌کند و هنگام تقسیم، به بالا گرد می‌کند.

در سالیدیتی، تقسیم همیشه به پایین گرد می‌شود. برای مثال، حاصل 10 / 3 برابر با ۳ است. اما اگر گرد کردن به بالا را اعمال کنیم، 10 / 3 برابر با ۴ خواهد شد.

هنگام محاسبه قیمت‌ها یا اعتبارها (credits)، باید همواره به نفع پروتکل و به ضرر کاربر گرد کنیم. برای مثال، اگر قصد داشته باشیم محاسبه کنیم که کاربر برای دریافت مقدار مشخصی از یک دارایی باید چقدر پرداخت کند، باید قیمت را به بالا گرد کنیم تا از منافع پروتکل محافظت شود.

برای مثال:

نتیجه 10 / 3 با گرد کردن به پایین برابر است با ۳.۳۳۳۳
نتیجه 10 / 3 با گرد کردن به بالا برابر است با ۳.۳۳۳۴ (بسته به اندازه مخرج)

گرد کردن به بالا یعنی اگر باقی‌مانده‌ی تقسیم غیر صفر باشد، ۱ واحد به نتیجه اضافه کنیم. برای نمونه، 9 / 3 = 3 دقیقاً برابر است و نیازی به گرد کردن وجود ندارد، بنابراین نباید ۴ را برگردانیم. اما 10 / 3 و 11 / 3 به ترتیب باقی‌مانده‌های ۱ و ۲ دارند، پس باید ۱ به نتیجه تقسیم اضافه کنیم.

در ادامه نحوه انجام این کار در کتابخانه Solmate آمده است:

در قسمت مشخص‌شده با زیرخط سبز، کد بررسی می‌کند که آیا باقیمانده تقسیم (modulo) بیشتر از صفر است یا نه. اگر این‌طور باشد، عدد ۱ به نتیجه اضافه می‌شود (یعنی گرد کردن به بالا انجام می‌شود). در غیر این صورت، عددی اضافه نمی‌شود و نتیجه به صورت عادی (بدون گرد کردن) بازگردانده می‌شود.

5/5 - (1 امتیاز)

راستی! برای دریافت مطالب جدید در کانال تلگرام یا پیج اینستاگرام سورس باران عضو شوید.

نظرات

برچسب ها: آموزش برنامه نویسی, آموزش سالیدیتی

آموزش انیمیشن‌ سازی دو بعدی با موهو – خلق انیمیشن‌ های خلاقانه شبیه دیرین دیرین

انتشار: ۹ خرداد ۱۴۰۴

آموزش محاسبات اعشاری ثابت در سالیدیتی + مثال

چرا عدد 10^{18} در سالیدیتی اهمیت دارد؟

تبدیل عدد صحیح به عدد اعشاری ثابت

ضرب دو عدد اعشاری ثابت

مثال کدنویسی برای ضرب اعداد اعشاری ثابت

مثال دنیای واقعی

ضرب یک عدد اعشاری ثابت در یک عدد صحیح

تقسیم اعداد اعشاری ثابت

تقسیم یک عدد اعشاری ثابت بر یک عدد صحیح

جمع و تفریق اعداد اعشاری ثابت

عدد اعشاری ثابت دودویی در مقابل ده‌دهی

کتابخانه اعداد اعشاری ثابت در Uniswap V2

تابع `encode()` در کتابخانه Uniswap V2

گرد کردن به بالا در مقابل گرد کردن به پایین

دسته بندی موضوعات

آخرین محصولات فروشگاه

نظرات

بازخوردهای خود را برای ما ارسال کنید

لغو پاسخ

مطالب مرتبط

چرا عدد 10^{18} در سالیدیتی اهمیت دارد؟

تبدیل عدد صحیح به عدد اعشاری ثابت

ضرب دو عدد اعشاری ثابت

مثال کدنویسی برای ضرب اعداد اعشاری ثابت

مثال دنیای واقعی

ضرب یک عدد اعشاری ثابت در یک عدد صحیح

تقسیم اعداد اعشاری ثابت

تقسیم یک عدد اعشاری ثابت بر یک عدد صحیح

جمع و تفریق اعداد اعشاری ثابت

عدد اعشاری ثابت دودویی در مقابل ده‌دهی

کتابخانه اعداد اعشاری ثابت در Uniswap V2

تابع encode() در کتابخانه Uniswap V2

گرد کردن به بالا در مقابل گرد کردن به پایین

دسته بندی موضوعات

آخرین محصولات فروشگاه

نظرات

بازخوردهای خود را برای ما ارسال کنید

لغو پاسخ

مطالب مرتبط

تابع `encode()` در کتابخانه Uniswap V2